구하고자 하는 식 입니다.
여기서 알수 있는 정보는
1.

즉

2.
(x2,y2) 는 ax + by + c = 0 위의 점이니 ax2 + by2 + c = 0
1 , 2 를 이용하면 원하는 거리를 구할 수 있습니다.
PQ = t OA 이므로
q - p = t a
(x2-x1,y2-y1) = t (a,b)
x2 -x1 = ta
y2 - y1 = tb
이를 위의 식에 대입하면
d = root ( t^2a^2 + t^2b^2) = |t| root( a^2 + b^2)
한 편
(x2,y2) 가 ax + by + c = 0 위의 점이므로
ax2 + by2 + c = 0
x2 = x1 + ta
y2 = y1 + tb
a(x1+ta) + b(y1+tb) + c
= ax1 + ta^2 + by1 + tb^2 + c
=ax1 + by1 +c + t(a^2 + b^2) = 0
그러므로 t = (-ax1 -by1 -c) / (a^2 + b^2) 이를 대입하면
d = |t| root(a^2 + b^2) 에 대입하면 원하는 결과가 나옴.
 [증명] 점과 직선사이 거리구하기(벡터 이용)
[증명] 점과 직선사이 거리구하기(벡터 이용)
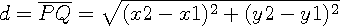
 즉
즉 