수(기타) 놀이터

|

문제 코너

|

제출 현황

|

수학 Q/A

|

수학 quiz

|

[벡터 이용] 평면에서 직선의 방정식 구하기

유일한 직선은 공간에서는  두 점이 주어지거나  

평면에서는 

• 한 점과  기울기가 주어지거나 
• 한 점과 구하고자 하는 직선과 수직인 벡터가 주어지면 유일한 직선을 구할 수 있습니다.

이 글은 한 점이 주어지고  수직인 벡터가 주어질 때 원하는 직선을 구하는 글 입니다.

Q(x,y) 에서 x,y 사이의 관계식을 끌어내면 됩니다.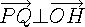

 

이므로 두 벡터의 내적값이 0 이 됩니다.

여기에서 주의해서 볼것은 (a,b) 에 수직인 직선의 방정식은 ax + by + 상수 = 0  꼴이 된다는 것을 알 수 있습니다.

어떤 직선 혹은 평면에 수직인 벡터를 법선 벡터라고 합니다. 

ax + by + c = 0 의 법선 벡터는 (a,b) 를 가집니다. 

참고: 벡터의 내적