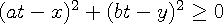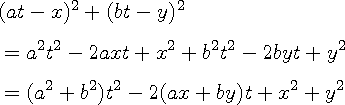다음 부등식은 어떤 값에도 성립하는 절대 부등식 입니다.
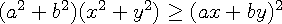
proof 1)
A > B 를 보여야 하는 경우
A - B 값이 양수이면 됩니다. 이를 이용한 증명 입니다.
ay = bx 일 때 등호가 성립 합니다.
일 때
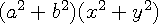
은 최소 값
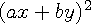
을 가집니다.
proof2)
판별식을 이용한 증명 입니다.
다음 부등식은 항상 성립합니다.
이를 t 에 대해서 풀면
이 식이 항상 0 이상이 되기 위해서는 D <= 0 가 되어야 합니다.
주의) a^2 + b^2 = 0 이면 (a=0 이고 b = 0) 이차식이 아니라서 판별식을 사용할 수 없지만 a=0 , b=0 을 대입하면 증명하고자 하는 부등식이 성립합니다.
 [증 명]코시 슈바르츠 부등식
[증 명]코시 슈바르츠 부등식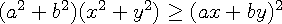
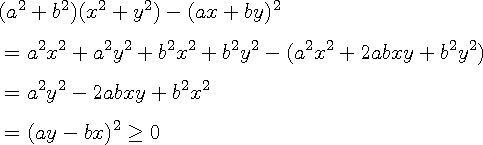
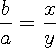
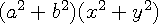 은 최소 값
은 최소 값 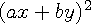 을 가집니다.
을 가집니다.