귀류법을 잘 이해할 수 있는 문제가 뭐가 있을까요?
그리고 대우 증명과의 차이를 나타내는 쉬운 문제가 뭐가 있을까요?
를 증명하는 방법.
2) 귀류법
의 진리 표(truth table) 입니다.( T:true , F:false)
진리표란? 가능한 모든 경우를 표시한 후의 참,거짓 상태 테이블을 말합니다. p 가 가질수 있는 상태는 참,거짓 , q 가 가질수 있는
상태를 참,거짓이므로 4 가지 상태를 만들 수 있습니다.
p -> q 의 진리표가 위와 같은 이유는 학교 다닐 때 이렇게 배웠습니다.
아버지가 아들에게 다음과 같은 약속을 하였습니다.
"날씨가 좋으면 놀이공원에 간다."
위의 진리표는 아들이 아버지에게 태클(?) 을 걸수 없으면 T 이고 , 아니면 F 입니다.
p: 날씨가 좋다
q: 놀이동산에 간다.
- 날씨가 안 좋아서 놀이 동산에 안갔다 ... 참
- 날씨가 안 좋았는데도 불구하고 놀이동산에 갔다.... 참
- 날씨가 좋았는데 놀이동산에 안갔다........ 거짓
- 날씨가 좋아서 놀이동산에 갔다.........참
를 not,or 연산으로 표현하면
와 같습니다.
이는 다음 진리표에서 확인할 수 있습니다.( or =
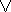
, and =
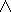
, not =
혹은
)
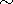
를 부정 해서 거짓 이라면
는 참이라고 할 수 있습니다. 이 증명 방법이 귀류법입니다.
즉 p 이고 q 가 아니다가 거짓임을 보이는 증명이 귀류법 입니다.
귀류법과 대우 증명의 몇가지 예를 보겠습니다.
보기)
이 짝수이면 x 도 짝수이다.
증명.
이 증명은 대우 증명과 귀류법의 차이를 잘 느끼지는 못합니다. 그래도 일단 예가 쉬우므로 한 번 해 보겠습니다.
- 대우 증명
원 명제의 대우 명제는
x 가 짝수가 아니라면
도 짝수가 아니다.
x = 2k +1 ( k 는 정수)
= 4k^2 + 4k + 1 = 2 (2k^2 + 2k) + 1
그러므로
도 짝수가 아니다##
- 귀류법
원 명제를 부정하면
이 짝수이고 x 는 짝수가 아니다.
이 명제가 틀렸다는 것을 보이면 됩니다.
and 조건이므로 둘다 참이어야 합니다.
x 는 짝수가아니다 --> x = 2k + 1
이를 제곱하면
= 2(2k^2 + 2k) + 1 이 홀수여서 거짓이 됩니다. 즉 부정한 명제가 거짓이므로 원 명제는 참##
p ->q
대우로 증명하는 방법은
~q -> ~p 를 보여야 하니 식을 푸는 시발점이 ~q 가 되어야 하지만
귀류법은
p ^ ~q 이므로 p 와 ~q 는 동등한 조건이므로 접근하기 쉬운 쪽으로 증명을 시작해도 되니
조금 더 넓은 용도에서 사용할 수 있습니다.
다른 예를 한 번 들어 보겠습니다.
보기) 인접한 정수는 서로 소이다.
증명.
귀류법으로 갑니다.
인접한 정수가 서로 소가 아니라고 하자.
n = Gm ... (1)
n+1=Gn (단 , G 는 1 이 아닌 정수... 서로 소가 아니라고 했으므로) ... (2)
(2) - (1) : 1 = G(n - m )
G 도 정수이고 n - m 도 정수이니 두 정수를 곱해서 1 이 되기 위해서는 모두 1 이 되어야 합니다.
그런데 G 는 1 이 아니라고 했으므로 거짓##
