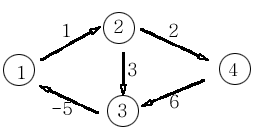
이 경우 1 -> 2 -> 3 -> 1 로 가면 음수이다. 이 경우 최단거리의 의미가 없으므로 음수 사이클을 인식하고 아닌 경우 최단거리를 구하는 프로그램을 구하려고 한다.
최단거리 문제에서 음수 사이클이 존재하면 사이클을 돌면 돌수록 최단거리가 만들어 지므로 최단거리를 개념자체 존재하지 않는다.또한 dijkstra 방법은 음수 가중치가 있는 경우에는 사용할수가 없다.
이 번에 알아볼 Bellman-Ford 알고리즘은 음수 가중치를 가지는 그래프에서 음수 사이클이 존재하는 경우 이를 알아낼수 있는 알고리즘이다. 방법은 dynamic programming 을 이용한다.
일반적으로 많이 이용하는 dp 접근 방법을 이용하니 dp 를 모르는 분들도 겸사겸사 한 번 해 보면 좋을듯.

이 경우 1 -> 2 -> 3 -> 1 로 가면 음수이다. 이 경우 최단거리의 의미가 없으므로 음수 사이클을 인식하고 아닌 경우 최단거리를 구하는 프로그램을 구하려고 한다.
설명을 위해 다음과 같이 가정
- 정점수 n = 4
- 출발 정점 1
- w[][] 각 정점간의 비용을 저장 즉 , w[2][3] = 3 , w[4][3]=6,....
- 먼저 점화 식 m[i][j] 는 출발지에서 i 개의 vertex 를 고려한 j 로 도착하는 최단 경로
- 최종적으로 출발지에서 도착지 k 로의 최단 경로는 m[4][k] 가 된다.(
n = 4 )
초기화
m[1,1]=0 m[1,2] , m[1,3] , m[1,4] 는 나올수 없는 경우
점화식.
그러므로 점화 m[i][j] 는
- m[2][4]: 2 개의 정점을 고려한 도착지가 4 인 경우 최단거리
m[2,4] 는 m[1][1] + w[1][4] m[1][2] + w[2][4] m[1][3] + w[3][4] m[1][4] + w[4][4] 중 최소값.- m[3][4]: 3 개의 정점을 고려한 도착지가 4 인 경우 최단거리
m[3][4] 는 m[2][1] + w[1][4] m[2][2] + w[2][4] m[2][3] + w[3][4] m[2][4] + w[4][4] 중 최소값.m[i][j] = min( m[i-1][k] + w[k][j] ) 단,k=1,2,...n
소스
#include <stdio.h>
int weight[100][100];
int d[100][100]; //d[i][j] 는 1 에서 i 까지의 vertex 를 고려한 소스에서 j 로 가는 최단 거리
int n; // vertex 의 수
int src; // 출발지
void init()
{
int i,j;
scanf("%d %d",&n,&src);
for(i = 1;i <= n;i++)
for(j = 1;j <= n;j++)
scanf("%d",&weight[i][j]);
}
void process()
{
int i,j,k,min;
for(i = 0; i<= n;i++)
d[0][i] = 9999999; //즉 d[i][j] = ∞
d[0][src]=0;
for(i = 1; i <= n;i++)
for(j = 1;j <= n;j++){
min = d[i-1][j];
for(k = 1; k <= n;k++)
if (d[i-1][k] + weight[k][j] < min) min = d[i-1][k] + weight[k][j];
d[i][j] = min;
}
}
void output()
{
int i,j;
//음수 사이클 check
//최적의 해를 구한 후 한 번 더 접근 한 값이 더 구한 최적의 해보다 좋으면 음수 사이클
for(i = 1; i <= n;i++)
for(j = 1;j <= n;j++)
if (d[n][i] + weight[i][j] < d[n][j] ){
printf("negative cycle\n");
return;
}
//최단 거리 출력
for(i=1;i<=n;i++){
printf("%4d",d[n][i]);
}
printf("\n");
}
int main()
{
init();
process();
output();
return 0;
}
-시간 복잡도:O(VE)