dp에서 자주 이용되는 확장 방법 입니다.

1. 구간수가 일정한 최대 합 풀이

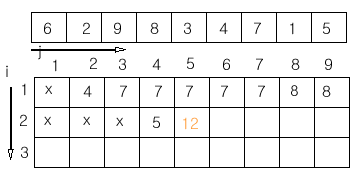
입력 데이터가 다음과 같고 3 구간으로 나눌 때의 최대값을 알아보겠습니다.

1	2	3	4	5	6	7	8	9
6	2	9	8	3	4	7	5	1

점화식을 정의 합니다.

• dy[i][j] ... i 개의 구간으로 나눌 때 1 .. j 까지의 구간의 최대 합으로 정의 합니다.
• 답은 max( dy[3][6], dy[3][7],dy[3][8] ,dy[3][9])

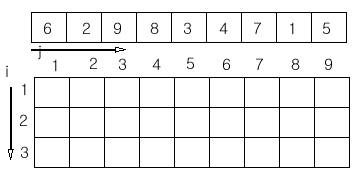
처음 테이블의 구조 입니다.

• 1 행 즉 한 구간일 때 눈으로 채워 봅니다.

  

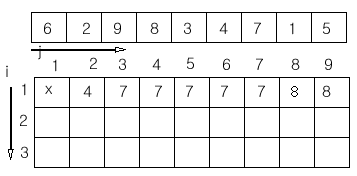
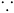• 다음 2 행에서1,2,3 열은 의미가 없습니다. ( 2 묶음으로 하기위해서는 4 개 이상의 수가 필요)

  2 행 4 열이 5 인 이유는 data[3],data[4] 를 한 묶음으로 하고 첫 행(한 묶음일 때의 구간) 에서 dy[1][2] 를 더한 값 입니다.

  

• 다음 2 행 5 열에서
  • data[4],data[5] 를 한 묶음으로 5 + dy[1][3] 7 = 12

    

  • data[3],data[4],data[5] 를 한 묶음으로 6 + dy[1][2] 4 = 10

    

  두 가지중 최대 12 가 저장됩니다.

  

• dy[2][6] 은 어떻게 채워 질까요?( data[a] ~ data[b] 는 a 에서 b 까지의 최대-최소값으로 약속하겠습니다.)
  • dy[1][4] + (data[5]~data[6])
  • dy[1][3] + (data[4]~data[6])
  • dy[1][2] + (data[3]~data[6])

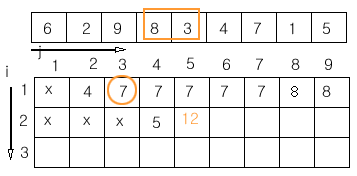
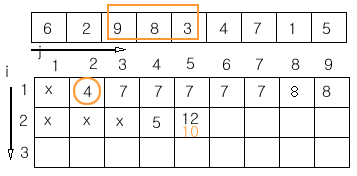
  이 중 최대값이 채워 집니다.

• ...

• 마지막 dy[3][9] 를 채워 보빈다.
  • dy[2][4] + data[5]~data[9]
  • dy[2][5] + data[6]~data[9]
  • dy[2][6] + data[7]~data[9]
  • dy[2][7] + data[8]~data[9]
  중 최대 입니다.

• max( dy[i-1][k] + data[k+1]~data[j] ), 단 k = 2*(i-1) ... j-2

2. 소스

#include <stdio.h>
int data[101];
int dy[51][101];

int diff(int m,int n)
{
   int i,max,min;

   max = min = data[m];

   for( i = m +1 ; i <= n ; i++){
      if ( max < data[i] ) max = data[i];
      if ( min > data[i] ) min = data[i];
   }

   return max - min;
}

int main()
{
   int i,j,k;
   int n,ng,max,tmp;

   scanf("%d %d",&n,&ng);

   for( i = 1 ; i <= n ; i++){
      scanf("%d",&data[i]);
   }

   for( i = 1 ; i <= ng ; i++){
      for( j = i*2 ; j <= n ; j++){
         max = -1;
         for( k = 2*(i-1) ; k <= j-2 ; k++){
            tmp = diff(k+1,j);
            if ( dy[i-1][k] + tmp> max ) {
               max = dy[i-1][k] + tmp;
            }
         }
         dy[i][j] = max;
      }
   }

   int ans=-1;

   for( i = ng*2 ; i <= n ; i++){
      if ( dy[ng][i] > ans ) ans = dy[ng][i];
   }

   printf("%d\n",ans);
}

3. 시간 복잡도

O(n^3)

출처:dovelet