http://59.23.113.171/pool/orthocenter/orthocenter.php?pname=orthocenter

문제구요

예전에 올릴려했는데 못올렸네요 ㅜㅜ

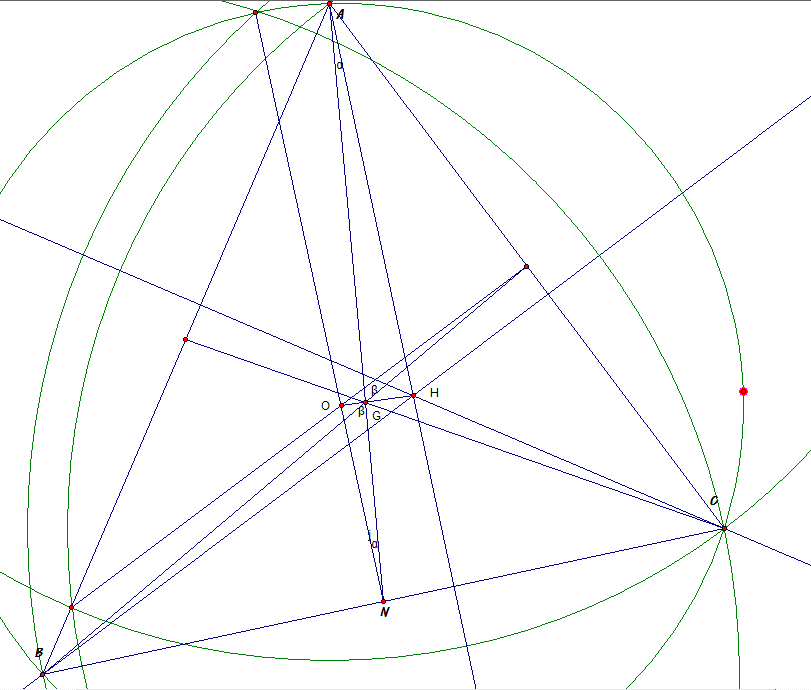
무게 중심의 성질에 의해

(∵두 선분의 혹은 그 연장선이 밑변과 수직으로 이루고 있으므로)

(∵엇각)

(∵맞꼭지각)

(∵AA닮음)

이므로 닮음비는 2:1 이고

∴이다.

그리고 이걸 Euler Line 이라 합니당;

http://blog.naver.com/rkdrjs0327/20144883811

제 증명입니다.. 언뜻 보니 코난님과 비슷하군요..

근데 증명에서 매우 중요한걸 놓치셔셨네요 ㅎ

저도 여기엔 그조건을 안써놨찌만 블로그 포스트에는 있어용 ㅎㅎ;;

*예각 삼각형* 이라는 조건이 있어야합니다..

직각,둔각인 경우는 특별한 경우만 성립하는걸로 알고있습니다. 증명을 안해봐서;

아 ㅋㅋ 빠뜨렸군요 감사합니다

그리고 그 증명을 안했다는게

"직각둔각인 경우는 항상 성립하지 않는다" 이거말한거에용 ㅎ