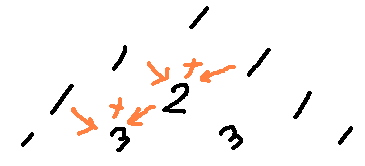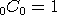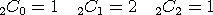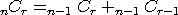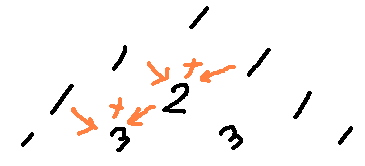
다음과 같은 모양의 삼각형을 파스칼의 삼각형이라 합니다.
각 행의 양 끝의 수는 1 이고 중 간에 있는 수는 바로 위 왼쪽 , 오른쪽 수의 합입니다.
첫 행의 1 은
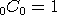
두 번째 행은

세 번째 행은
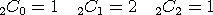
...
그러면 왜 위 왼쪽 , 오른쪽의 합으로 삼각형을 만들어 갈까요?
이는 조합의 다음과 같은 점화식의 성질 때문 입니다.
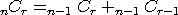
n 개 중에 r 개를 선택하는 경우의 수 = ( n-1 개 중에 r 개를 선택) 하거나 (n-1 개 중에 r-1 개를 선택하는 경우)
왜 그럴까요? 이 부분 조금 생각을 해야 합니다.
설명의 편의를 위해 4 개 중에 3 개를 선택하는4C3 으로 설명을 해 보겠습니다.
즉 주머니에 1 ,2,3,4 가 쓰여진 구슬이 있는 경우 3 가지를 뽑는 경우의 수 입니다. 물론 답은 4 가지 입니다.
1 2 3
1 2 4
1 3 4
2 3 4
여기에서 1 번 구슬에 초첨을 맞추겠습니다.
4 개중 3 개를 선택할 때 1 번 구슬을 포함하거나 혹은 포함하지 않는 경우로 나눌 수 있습니다. or 조건 입니다. 두 가지 경우를
구한후 결과를 더해 주어야 합니다.
3 개 중에 1 번 구슬을 포함하는 경우 + 3 개 중에 1 번 구슬을 포함하지 않을 경우 - 3 개 중에 1 번 구슬을 포함하는 경우는 2 , 3 , 4 중에 2 개를 포함하는 경우이고 3C2
- 3 개 중에 1 번 구슬을 포함하지 않는 경우는 2 , 3, 4 중에 3 개를 선택하는 경우입니다. 3C3
4C3 = 3C2 + 3C3 으로 설명 할 수 있습니다.
참고: 부분 집합의 갯수
 파스칼 의 삼각형
파스칼 의 삼각형