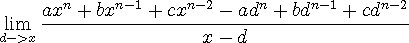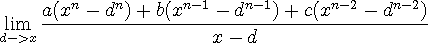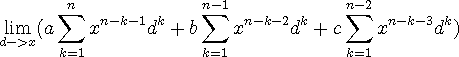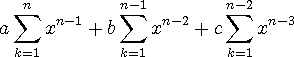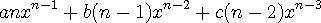+로 내용 달겠습니다. 잘 다듬어서 이어주세요. ^^
그렇다면, 이 정보를 어떻게 활용해야 우리가 유익하게 사용할 수 있을까??
가장 좋은 것은 기울기를 구할 수 있도록 일반항화 시키는 것이다.
위에서 활용한 바와 같이, 두 점을 잡고 극한으로 보내주면 된다.
임의의 한 x좌표를

, 다른 x좌표를

라 하자.
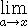
로 보낸다 하였을 때 위의 식
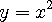
의 기울기는 다음과 같이 구할 수 있게 된다.
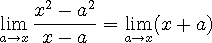
,

따라서 우리가 구하려는 기울기 함수는
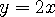
가 된다.
좀 더 구체적으로 해서, 미분 방법을 이해해보자.
임의의 식
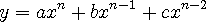
의 기울기 함수를 구해보자.(편의상 더 길게는 무리)
같은 항끼리 묶어준다면
위의 식을 전부 간단하게 풀어준다면, (편의상 시그마를 활용하겠습니다.)
이 된다. d->x 가 된다 하였으므로, 모든 식이 간결하게 묶이게 된다.
이제 상수 k는 시그마 함수 내에서 무관해졌으므로, 더 간단히 정리가 된다.
이것을 보고 미분을 하는 일반적인 방법을 찾아낼 수 있지 않을까??
------------------
쓰고 나니 참 기네요... -_- 더 진행 안하신 이유를 알겠네요.
 [개념] 미분이 뭐꼬?^^
[개념] 미분이 뭐꼬?^^
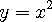 위의 (1,1) 지점에서 접선의 방정식을 구하는 문제로 접근해 보겠습니다.
위의 (1,1) 지점에서 접선의 방정식을 구하는 문제로 접근해 보겠습니다.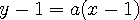
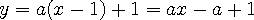
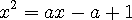
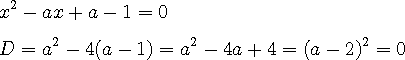
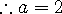

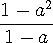
 ) 시켜 버리면 (1,1) 에서의 기울기가 될 것이다
) 시켜 버리면 (1,1) 에서의 기울기가 될 것이다 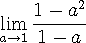
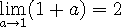
 로 표시하고 이는 x 점에서 접선의 기울기를 의미 합니다.
로 표시하고 이는 x 점에서 접선의 기울기를 의미 합니다. , 다른 x좌표를
, 다른 x좌표를  라 하자.
라 하자.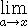 로 보낸다 하였을 때 위의 식
로 보낸다 하였을 때 위의 식 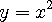 의 기울기는 다음과 같이 구할 수 있게 된다.
의 기울기는 다음과 같이 구할 수 있게 된다.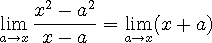 ,
, 
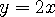 가 된다.
가 된다.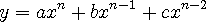 의 기울기 함수를 구해보자.(편의상 더 길게는 무리)
의 기울기 함수를 구해보자.(편의상 더 길게는 무리)