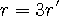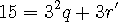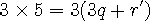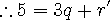나머지 정리에서 자주 나오는 문제인데 왜 이렇게 풀수 있는지 수로 고민 한 번 해 봤습니다.
(문제)
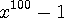
을
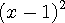
으로 나눈 나머지를 구하여 보자.
풀이.
이차식으로 나누므로 나머지는 일차식 이하 입니다.
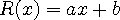
이므로
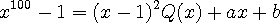
.......................(1)
양번에 1 을 대입하면
이를 (1) 식에 대입하면

이므로
밑줄 친 식에 1 을 대입하면 a 는 100 , b = -100 해서 나머지를 구할 수 있음.
그런데 이런 식으로 유도할 수 있는 것은 식으로는 아래와 같이 이해할 수 있습니다. ( 틀리면 알려 주세요.)
15 를 9 로 나눈 나머지를 구하여 봅니다. ( 나머지는 6 이지만 위 식과 연관시켜 보려 합니다)
여기에서 9 는 3^2 이고 문제가 성립하기 위해서는 15 는 3 으로 나누어 져야 합니다.
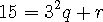
......(1)
15 는 3 으로 나누어 지므로 나머지가 0 입니다. 우변도 3 으로 나누어져야 하므로 r 은 3 의 배수가 되어야 합니다.
이를 (1) 식에 대입하면
5 는 3 으로 나눈 나머지가 2 이므로 r' 도 2 가 되어야 합니다.
구하고자 하는 r = 6 이 됩니다.
 [개념] 제곱 꼴의 나머지 정리
[개념] 제곱 꼴의 나머지 정리 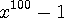 을
을 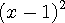 으로 나눈 나머지를 구하여 보자.
으로 나눈 나머지를 구하여 보자.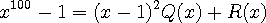
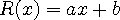 이므로
이므로 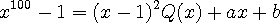 .......................(1)
.......................(1)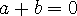
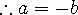
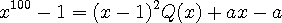
 이므로
이므로 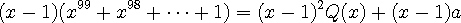

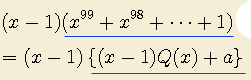
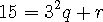 ......(1)
......(1)