| 30 계단 | | | 옥 상 | | | 제출 현황 | | | Ranking | | | FAQs | | | 오류보고 | | | QandA | | | 푼 후 | | | 자유게시판 | | |
 nCr 구하기
nCr 구하기 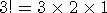
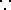 즉 첫 수는 1,2,3 중 세 개의 수가 올수 있고 두 번째 수는 첫 번째 수를 제외한 수 2 가지 ,3 번째 자리는 첫번째 , 두번째 자리를 제외한 수 1 가지가
즉 첫 수는 1,2,3 중 세 개의 수가 올수 있고 두 번째 수는 첫 번째 수를 제외한 수 2 가지 ,3 번째 자리는 첫번째 , 두번째 자리를 제외한 수 1 가지가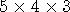
 첫수는 5 개의 수 중 5 개 , 두 번째 수는 나머지 수 중 4 , 세 번째 수는 3 개
첫수는 5 개의 수 중 5 개 , 두 번째 수는 나머지 수 중 4 , 세 번째 수는 3 개 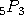



음 글자 색깔이 자동으로 칠해져 있네요;;
begin{displaymath}
end{displaymath}x^{2}begin{displaymath}
end{displaymath}
수식을 누르고, x^2 을 누르고 중괄호 안에 2를 넣으면 바로 이렇게 뜨고  이 표시만 반복됩니다.
이 표시만 반복됩니다.
여기서 end{displaymath} begin{displaymath} 를 지워주면  이렇게 뜨게 됩니다.
이렇게 뜨게 됩니다.
불필요한 두 줄이 수식 삽입 과정에서 들어가있는듯합니다. 제가 실험을 해 본 결과로는 이렇습니다.
[내용] 이 있는 상태에서 수식을 누르면, [내용]수식[내용] 이런 형태로 붙여넣기가 되는듯합니다.