제곱 근이란 ?
(1) 다음 방정식의 근은 뭘까요?
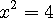
(sol)
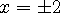
이 근을 4 의 제곱근이라 합니다. 4 의 제곱은
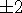
입니다.
(2) 다음 방정식의 근은 ?
(sol)
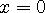
. 즉 0 의 제곱근은 0 입니다.
(3) 다음 방정식의 근?
(sol) 같은 수를 곱하면 + 곱 + = + 이고 , - 곱 - = + 가 되니 음수를 만들수는 없습니다.
-4 의 제곱곱은 없습니다. 빵 개
정리하면 양수의 제곱근은 2 개 , 0 의 제곱근은 1 개 , 음수의 제곱근은 0 개 입니다.
양수의 제곱근 두 개 중 양수를 양의 제곱근 , 음수를 음의 제곱근이라 합니다.
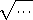 기호의 도입.
기호의 도입.
4 의 제곱근은 2 , -2 입니다. 그러면 5 의 제곱근은 무엇일까요?
제곱하여 5 가 되는 수?
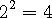
이고
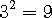
이 2 와 3 사이의 수가 된다는 것은 알 수 있습니다. 2 와 3 사이 중간 지점
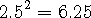
다시 반을 나누고 ....
>>> 2.2**2
4.8400000000000007
>>> 2.3**2
5.2899999999999991
가 되니 2.2xxx 가 됩니다. 이렇게 다시 다음 수를 구하는 과정을 거치면서 내년 추석때까지 계산을 하더라도 끝이 나질 않습니다.
이 수를 다 쓸수도 없고 설명 쓴다고 하더라도 너무 깁니다. 그래서 도입 한 것이
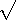
(root 의 첫 글자 r, 루트라 읽습니다) 기호 입니다.
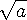
를 제곱해서 a 가 되는 수 중 양수 즉
a 의 양의 제곱근으로 약속 합니다.
그러면
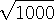
은 어떤 정수 사이에 있을까요?
개평 법

를 소수 이하 세자리까지 구하여 보자.
먼저
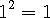
이고
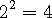
이니
여기서 사용된 개념은 두 가지 입니다.
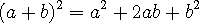 과 그리디 메소드로 구할 수 있습니다.
과 그리디 메소드로 구할 수 있습니다.
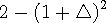
에서 2 를 넘지 않는

를 구해야 합니다.

는 소수이하 한자리 수 입니다.
여기에서 조금 생각해야 합니다.
에서
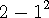
은 위에서 계산한 결과를 이용합니다.

를 빼주면 됩니다. 그런데

는 소수이하 한자리 수 ...... 제곱하면 소수이하 두 자리가 나옵니다.
그러므로 일반 나눗셈과는 다르게 0 을 두개 붙인 후 적절히 빼주어야 합니다.
이제 100 -

을 해야 합니다.
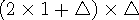
는 다음 꼴로 만들수 있습니다.
2 x 1 이니 1 + 1 을 한 후 100 을 넘지 않는

를 구하면 됩니다.
1
1
---
2

구한

는 다음과 같습니다.
다음 수는 위의 과정의 반복 입니다. 1.414 ...... ##
 [개념] 제곱 근 + 계평 법
[개념] 제곱 근 + 계평 법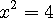
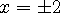
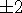 입니다.
입니다.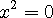
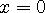 . 즉 0 의 제곱근은 0 입니다.
. 즉 0 의 제곱근은 0 입니다.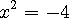
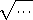 기호의 도입.
기호의 도입.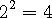 이고
이고 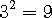 이 2 와 3 사이의 수가 된다는 것은 알 수 있습니다. 2 와 3 사이 중간 지점
이 2 와 3 사이의 수가 된다는 것은 알 수 있습니다. 2 와 3 사이 중간 지점 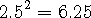
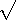 (root 의 첫 글자 r, 루트라 읽습니다) 기호 입니다.
(root 의 첫 글자 r, 루트라 읽습니다) 기호 입니다.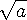 를 제곱해서 a 가 되는 수 중 양수 즉 a 의 양의 제곱근으로 약속 합니다.
를 제곱해서 a 가 되는 수 중 양수 즉 a 의 양의 제곱근으로 약속 합니다.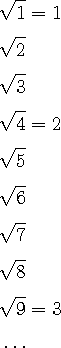
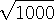 은 어떤 정수 사이에 있을까요?
은 어떤 정수 사이에 있을까요?  를 소수 이하 세자리까지 구하여 보자.
를 소수 이하 세자리까지 구하여 보자.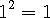 이고
이고 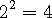 이니
이니 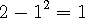
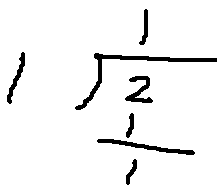
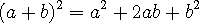 과 그리디 메소드로 구할 수 있습니다.
과 그리디 메소드로 구할 수 있습니다.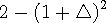 에서 2 를 넘지 않는
에서 2 를 넘지 않는  를 구해야 합니다.
를 구해야 합니다.  는 소수이하 한자리 수 입니다.
는 소수이하 한자리 수 입니다.
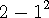 은 위에서 계산한 결과를 이용합니다.
은 위에서 계산한 결과를 이용합니다. 를 빼주면 됩니다. 그런데
를 빼주면 됩니다. 그런데  는 소수이하 한자리 수 ...... 제곱하면 소수이하 두 자리가 나옵니다.
는 소수이하 한자리 수 ...... 제곱하면 소수이하 두 자리가 나옵니다.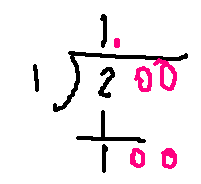
 을 해야 합니다.
을 해야 합니다.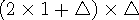 는 다음 꼴로 만들수 있습니다.
는 다음 꼴로 만들수 있습니다.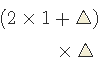
 를 구하면 됩니다.
를 구하면 됩니다.

 는 다음과 같습니다.
는 다음과 같습니다.
 에서 2 를 넘지 않는
에서 2 를 넘지 않는  를 구해야 합니다.
를 구해야 합니다.  는 소수이하 한자리 수 입니다.
는 소수이하 한자리 수 입니다. 의 값의 계산을 쉽게 하기 위해, 모든 항에 100을 곱합니다. ( 결과적으로 제곱 안에는 10이 곱해져, 소수점이 없어지게 됩니다.)
의 값의 계산을 쉽게 하기 위해, 모든 항에 100을 곱합니다. ( 결과적으로 제곱 안에는 10이 곱해져, 소수점이 없어지게 됩니다.) (
(  =
=  의 소수 첫째자리 숫자) 이 식의 제곱을 풀어주면
의 소수 첫째자리 숫자) 이 식의 제곱을 풀어주면 이 되고, 이 식을 최종 정리해주면
이 되고, 이 식을 최종 정리해주면 이 됩니다.
이 됩니다. 의 값은 4가 되고, 다음 과정을 계속해서 반복합니다.
의 값은 4가 되고, 다음 과정을 계속해서 반복합니다.