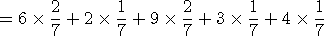기대값을 왜 평균이라 하는지 얼마전에 알았습니다. 

예를 들어 ,  한 반이 7 명이고 수학 점수가 아래와 같다면 

6 , 2 . 9 , 6 , 3 , 4 , 9

수학 점수의 기대값을 구하라고 하면   

답은  (6 + 2  + 9 + 6 + 3 + 4 + 9)/7 이 됩니다.

어라.....기대값을 구하라 했는데 평균을 구하는 것이  이상하게 보이나요. 하지만 기대값이 맞습니다.

왜냐하면 

6 점은 총 7 개의 점수 중에 2 개가 있고 

2 점은  1 개

9 점은 2 개 

3 점은 1 개 

4 점은 1 개

기대값을 구하는 공식은 다음과 같습니다. 각 변량에 확률을 곱한 누적 합 입니다.

  

이 식은 (6 + 2  + 9 + 6 + 3 + 4 + 9)/7 와 같습니다.

<재미있는 천재들의 수학퍼즐 1>에서 나온 것이 있죠.

(베르누이의 역설이던가..)

동전을 1번 던져서 앞면이 나오지 않으면 1페니를 주고, 2번째 던질때까지 앞면이 나오지 않으면  2페니를 주고, ... n번째 던질때까지 앞면이 나오지 않으면 2^n-1페니를 주고,...

를 앞면이 나올때까지 시행한다고 합시다.

기대값은 놀랍게도 무한! (1/2 + 1/2 + 1/2 + ....)가 됩니다.

하지만 여기에 100페니이상 걸고 도박을 할 사람은 별로 없겠죠.

이렇게 해서 무한대가 된다란 것은 이해가 되는데 

이 것이 왜 재밌는  문제인지 이해가 잘 되지 않네요ㅜㅜ

즉 사람의 도박 욕구와 기대값은 비례하지 않는다는 이야기가 됩니다. ㅋ