동적 계획법을 모르는 경우에는 가장 가까운 경찰차들을 순차적으로 보내며 처리하는 O(N) Greedy method 방법 , 모든 차들을
해당 위치로 배치해 보는 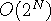 Brute-Force 한 방법이 떠 오를 것이다.
Brute-Force 한 방법이 떠 오를 것이다.
하지만 Greedy method 는 최적의 정답이란 보장이 존재하지 않기에 올바른 정답이 나오지 않을 것이고 ,
Brute-Forece 한 방법으로 접근 시 N 의 제한으로 인해 시간초과가 나올 것이다.
이러한 경우에 우리는 동적 계획법을 사용한다. 점화식을 소개한다.
dp[i][j] = i 번째 위치와 j 번째 위치에 경찰차가 있을때의 최적의 비용(i > j )
즉 i 번째 위치까지 최적으로 값을 구한다는 것을 의미한다. 이 때 i+1 번째 위치를 최적으로
구하는 데에는 두 가지 접근이 있다.
- j 는 그대로 있고 , i 에서 i+1 로 이동하는 경우 : dp[i+1][j] = dp[i][j] + cost[i][i+1]
- i 는 그대로 있고 , j 에서 i+1 로 이동하는 경우 :dp[i+1][i] = opt ( d[i+1][i] , d[i][j] + cost[j][i+1])
(cost[a][b] : a 에서 b 로 이동하는데 드는 최소 비용)
여기서 opt 는 최솟값을 구할 경우 min 함수로 최댓값을 구할 경우 max 함수를 사용하면 된다.
구조는 이중 반복문이며 , 반복문 안에 반복문이 2 개가 사용되는 구조이다.
위의 문제로 경로 추적을 제외한 최적의 비용만을 짠다면 다음과 같다. 0 번째 위치는 (1,1),
1 번째 위치는 (n,n) 으로 초기 경찰차들의 위치를 저정하였다고 가정한다.
for( i = 2 ; i < W + 2 ; i++)
{
for( j = 0 ; j+1 < i ;j++) dp[i][j] = dp[i-1][j] + cost[i-1][i];
for( j = 0 ; j+1 < i; j++) dp[i][i-1]=min( dp[i][i-1],dp[i-1][j] + cost[j][i];
}
따라서 시간 복잡도는 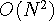 이다.
이다.
written by Fate
 경찰차 첨부 문서 입니다.
경찰차 첨부 문서 입니다.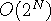 Brute-Force 한 방법이 떠 오를 것이다.
Brute-Force 한 방법이 떠 오를 것이다.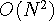 이다.
이다.