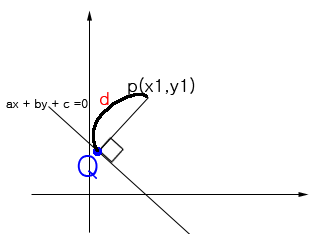
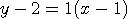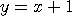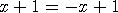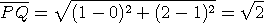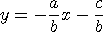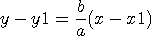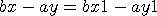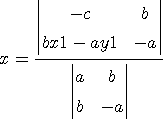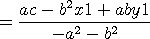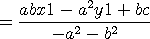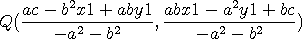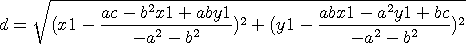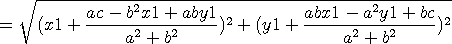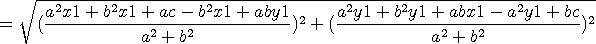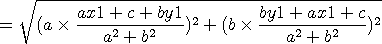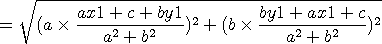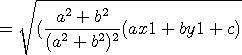직선 위에 있지 않은 한 점 P(x1 ,y1) 에서 직선 ax + by + c = 0 사이의 거리 구하는 공식 증명
proof) 이 증명을 하기 전에 구체적인 수를 넣은 후 거리를 구하고 이 공식을 증명해 보겠습니다.
(식이 복잡해서 그렇지 제 생각에는 이 증명이 가장 쉬운것 같습니다.)
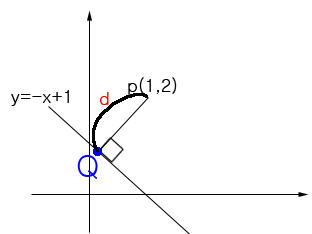
그림에서 d 를 구하여 보자.
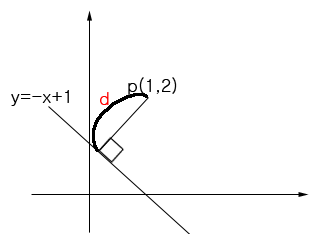
교점의 Q를 구하면 PQ 사이의 거리를 구할 수 있습니다. Q 점을 구하겠습니다.
step1. 기울기의 곱이 -1 이므로 P 점을 지나는 직선의 기울기는 1
step2. 이 직선이 (1,2) 를 지나므로
step3. 두 직선과의 교점이 Q 이므로
그러므로 x = 0 , y = 1
P(1,2) , Q(0,1) 이므로 두 점사이의 거리는
이 과정을 문자로 끌어 보면 위의 공식이 나옵니다.
식이 조금 복잡해지니 심호흡을 한 번 하고 갑니다.
step1.
ax + by + c = 0 을 표준형으로 고치면
P 점을 지나는 직선의 기울기는
step2. P 점을 지나는 직선의 방정식은
step3. 두 직선의 교점 Q 는
crammer 의 법칙을 적용하면
step4. 두점 P,Q 사이의 거리 d 는
ax1 + by1 + c 로 묶으면
점과 직선 사이의 거리 구하기
