우선은 L이 고정된 경우에 대해 생각해보자. 책의 순서가 정해져 있으므로 전형적인 동적 계획법 문제가 된다.
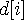 를 1~i번째의 책을 꽂을 때 책장 높이의 최소값이라 정의하면,
를 1~i번째의 책을 꽂을 때 책장 높이의 최소값이라 정의하면,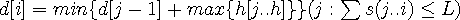 의 점화식을 얻는다. 이 때의 시간복
의 점화식을 얻는다. 이 때의 시간복잡도는
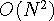
이다. 하지만 시간복잡도를
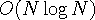
으로 줄일 수 있다.
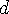
가 단조증가하므로
고정된
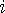
값에 대해
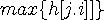
가 같다면 가장 작은
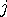
에 대해서만 보면 된다.
즉,
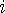
에서부터 앞으로 오면서
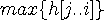
의 값을 더 크게 만드는
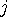
에 대해
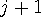
에 대해서만 봐도 된
다.
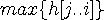
값을 더 크게 만든다는 것은
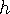
값이
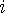
까지의 자기 뒤의 모든 것보다 큼을
의미하므로 그러한 지점을 저장하기 위해 스택을 이용한다.
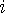
에 대해 스택의 위에서부터 보면서 현재보다 작은 것들을 다 빼내고
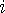
를 집어넣는다.
스택을 관리하면서 스택에 든
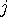
에 대해 바로 다음의
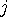
에 대해서는 알맞은
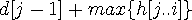
값으로 갱신 해주고 나머지
값은 무한대로 저장한다.
인덱스 트리를 이용하여
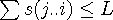
를 만족하는 구간에서의 최소값을 구하고 구간 가장 앞의 j에서도 최소가 될 수 있으므로 비교해서 최소값을 구한다.
이제 고정된
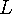
에 대해 최소의
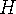
를 구하는 문제는 해결된다.
본 문제는
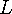
과
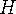
중 큰 값을 최소화하는 문제인데
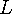
이 증가함에 따라 최소의
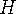
가 단조감소하므로
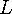
과
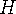
의 최대값은 쭉 감소하다가 최소가 되는 지점부터 다시 증가하므로 이분검색을 사용하여 최소가 되는 점을 찾을 수 있다.
이런 식으로 하면 총 시간복잡도
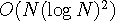
로 해결
 koi book 대회 풀이
koi book 대회 풀이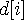 를 1~i번째의 책을 꽂을 때 책장 높이의 최소값이라 정의하면,
를 1~i번째의 책을 꽂을 때 책장 높이의 최소값이라 정의하면,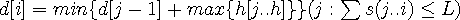 의 점화식을 얻는다. 이 때의 시간복
의 점화식을 얻는다. 이 때의 시간복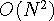 이다. 하지만 시간복잡도를
이다. 하지만 시간복잡도를 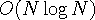 으로 줄일 수 있다.
으로 줄일 수 있다. 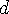 가 단조증가하므로
가 단조증가하므로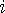 값에 대해
값에 대해 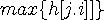 가 같다면 가장 작은
가 같다면 가장 작은 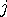 에 대해서만 보면 된다.
에 대해서만 보면 된다. 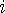 에서부터 앞으로 오면서
에서부터 앞으로 오면서 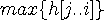 의 값을 더 크게 만드는
의 값을 더 크게 만드는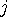 에 대해
에 대해 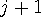 에 대해서만 봐도 된
에 대해서만 봐도 된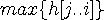 값을 더 크게 만든다는 것은
값을 더 크게 만든다는 것은 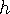 값이
값이 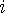 까지의 자기 뒤의 모든 것보다 큼을
까지의 자기 뒤의 모든 것보다 큼을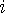 에 대해 스택의 위에서부터 보면서 현재보다 작은 것들을 다 빼내고
에 대해 스택의 위에서부터 보면서 현재보다 작은 것들을 다 빼내고 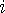 를 집어넣는다.
를 집어넣는다. 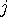 에 대해 바로 다음의
에 대해 바로 다음의 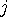 에 대해서는 알맞은
에 대해서는 알맞은 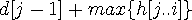 값으로 갱신 해주고 나머지
값으로 갱신 해주고 나머지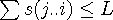 를 만족하는 구간에서의 최소값을 구하고 구간 가장 앞의 j에서도 최소가 될 수 있으므로 비교해서 최소값을 구한다.
를 만족하는 구간에서의 최소값을 구하고 구간 가장 앞의 j에서도 최소가 될 수 있으므로 비교해서 최소값을 구한다.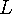 에 대해 최소의
에 대해 최소의 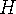 를 구하는 문제는 해결된다.
를 구하는 문제는 해결된다.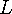 과
과 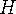 중 큰 값을 최소화하는 문제인데
중 큰 값을 최소화하는 문제인데 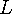 이 증가함에 따라 최소의
이 증가함에 따라 최소의 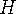 가 단조감소하므로
가 단조감소하므로 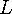 과
과 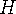 의 최대값은 쭉 감소하다가 최소가 되는 지점부터 다시 증가하므로 이분검색을 사용하여 최소가 되는 점을 찾을 수 있다.
의 최대값은 쭉 감소하다가 최소가 되는 지점부터 다시 증가하므로 이분검색을 사용하여 최소가 되는 점을 찾을 수 있다. 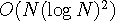 로 해결
로 해결