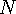좌표평면에 3개씩 개의 그룹으로 묶여 있는  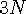개의 선분이 주어진다. 각 그룹에서 최대 하나의 선분을 제거할 수 있을 때, 남은 선분들 사이에 교점이 없도록 만들 수 있는 지 결정하는 것이 문제이다.

 각 그룹마다 3가지의 가능성이 있으므로 모든 경우를 시험해보면 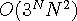 의 시간이 걸리지만, 이보다 더 효율적인 방법이 존재한다. 한 그룹 내에 있는 세 선분을  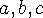라고 하자. 

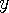어느 한 선분을 지우게 되면 다른 두 선분은 남겨둬야 한다. “를 지움”이라는 명제를 기호 로 나타내고, 비슷한 방법으로 와 를 정의하면, 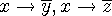를 포함한 함축(implication) 6개를 얻게 된다. 

서로 교차하는 두 선분 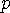와 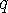에 대해서도 같은 방법으로 “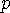를 지우지 않으면 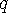를 지워야 함,” “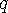를 지우지 않으면 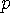를 지워야 함”의 implication 쌍을 얻게 된다. 이 모든 함축(implication)을 만족하는 해를 찾는 것은 2-SAT 문제이다. 강연결 요소(Strongly Connected Component: SCC)와 위상정렬을 이용하면 함축(implication) 그래프의 크기에 비례하는 시간에 답을 구할 수 있다. 

전체적인 수행시간은 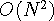 이다.