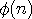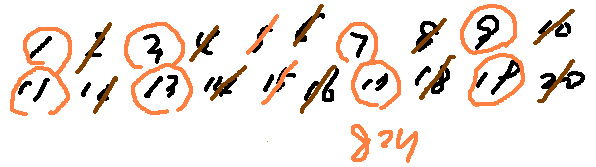오일러 totient 함수란?
n 보다 작은 수 중 n 과 서로 소인 수의 갯수 구하는 함수.
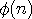
pi 는 n 의 소인수.
예를 들어 n 이 20 인 경우
proof)
1 에서 20 까지의 수 중 2 의 배수는 개수는 10 개 입니다.
20 - 20/2 = 20(1 - 1/2) = 10 개
남은 10 개의 수는
1 , 3 , 5 , 7 , 9 , 11 , 13 ,15 , 17 , 19
입니다.
이 중 5 의 배수의 갯수는 두개가 있습니다.
10 - 10/5 = 10(1-1/5)= 8 개
작업중....
 오일러 totient 함수
오일러 totient 함수