포함과 배제의 원리

삭제 | 편집 | 답글

합집합의 갯수를 구할 때 한 번은 포함(더하고) 한번은 배제(빼는)하는 것을 포제의 원리 혹은 포함과 배제의 원리라고 합니다.

-------------- ------------

포함 배제

-------------------- -------------------------------- --------------

포함 배제 포함

포함 , 배제 , 포함 , 배제가 됩니다.

일단 왜 이리 되는지를 알아보기전에 그대로 식을 적용해서 그렇게 되는지 부터 알아 보겠습니다.

작업 중....

2011-09-27 16:54 , testid

삭제 | 편집 | 답글

증명) 집합 A1,A2,...,An 원소 a1,a2,...,am

임의의 원소 ai는 A1,A2,..,An중 k개에 포함된다고 가정하자.

k=0일 경우 0번 카운팅되므로 성립.

k>=1일 경우 k개 집합에 포함되므로 카운팅 횟수는

kC1-kC2+kC3-kC4+...+((-1)^(k+1))*kCk가 된다.

그런데 kC0-kC1+kC2-kC3+kC4-...+((-1)^k)*kCk)=0.(이것은 (1-1)^k의 전개식과 같으므로 성립.)

kC0=1이므로 kC1-kC2+kC3-kC4+...+((-1)^(k+1))*kCk=1

따라서 k>=1일경우 ai는 1번 카운팅됨.

따라서 이렇게 카운팅하면(원래 합집합 기호를 시그마처럼 써서 하면 쉬운데 약간 식으로 나타내기 까다로워졌네요)

n(

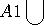
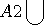
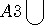
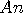)을 구할 수 있게 됩니다.

2011-09-27 19:44 , ainta

삭제 | 편집 | 답글

이해가 안되요. 조금 자세하게 가르쳐 주세요.

2011-09-27 20:03 , testid

삭제 | 편집 | 답글

k>=1일 경우 k개 집합에 포함되므로 카운팅 횟수는

kC1-kC2+kC3-kC4+...+((-1)^(k+1))*kCk가 된다.

이 부분이 이해가 안되신다는거죠?

그 다음줄은 이항정리로 바로 성립합니다.

이 부분은 ai가 k개 집합에 포함되면

n(A1)+n(A2)+...+n(An)에서 k번 세지고(kC1번)

마찬가지 방법으로 하면 됩니다.

2011-09-27 20:16 , ainta

삭제 | 편집 | 답글

집합 A1,A2,...,An 원소 a1,a2,...,am 에서 ai 가 임의의 원소 인가요?

2011-09-27 20:17 , testid

삭제 | 편집 | 답글

임의의 원소라고 써져 있는데요?

2011-09-27 20:19 , ainta

삭제 | 편집 | 답글

혹 잘못 쓴것이 아닌가 해서요.

조금 생각해보고 이해안되면 다시 질문하겠습니다.고맙 습니다.

2011-09-27 20:26 , testid