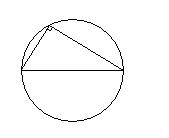
원의 지름을 빗변으로 하는 삼각형은 무조건 직각삼각형이다. 라는 것은 익히 들어서 알고 있을 수 있습니다.
피타고라스에서 익숙해졌을수도 있고, 중학교때 도형다루는 것에서 익숙할 수도 있는 내용이지요.
그렇다면, 이것이 왜 90도인지를 증명해보겠습니다.
다음과 같이 원의 중심에서 원 위의 임의의 한 점을 찍고 삼각형을 그어준다면,
원의 중심에서 각 꼭지점까지의 거리는 반지름으로 동일하게 됩니다.
이 그림에서 우리는 2가지의 특징만으로 90도임을 손쉽게 증명할 수 있습니다.
1. 이등변삼각형의 정의 : 두 변의 길이가 같은 삼각형
-> 특징 : 두 밑각의 크기가 같다.
2. 삼각형의 세 각의 합은 180도이다.
만들어지는 임의의 두 삼각형의 한 밑각을 각각
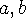
라 정의한다면,
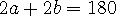
이 성립한단걸 알 수 있고,
결론적으로
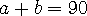
임을 알 수 있습니다.
그러므로 우리는 임의의 한 점의 각도가 어느 위치에든 상관없이 90도임을 증명할 수 있습니다.
막상 하고보니 증명같지도 않고, 모두가 알고 있는 지식을 괜히 포장만 한거 같네요.
 원의 지름을 빗변으로 하는 삼각형은 무조건 직각삼각형이다. 라는 것은 익히 들어서 알고 있을 수 있습니다.피타고라스에서 익숙해졌을수도 있고, 중학교때 도형다루는 것에서 익숙할 수도 있는 내용이지요.그렇다면, 이것이 왜 90도인지를 증명해보겠습니다.
원의 지름을 빗변으로 하는 삼각형은 무조건 직각삼각형이다. 라는 것은 익히 들어서 알고 있을 수 있습니다.피타고라스에서 익숙해졌을수도 있고, 중학교때 도형다루는 것에서 익숙할 수도 있는 내용이지요.그렇다면, 이것이 왜 90도인지를 증명해보겠습니다.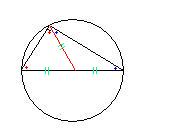 다음과 같이 원의 중심에서 원 위의 임의의 한 점을 찍고 삼각형을 그어준다면,원의 중심에서 각 꼭지점까지의 거리는 반지름으로 동일하게 됩니다.이 그림에서 우리는 2가지의 특징만으로 90도임을 손쉽게 증명할 수 있습니다.1. 이등변삼각형의 정의 : 두 변의 길이가 같은 삼각형-> 특징 : 두 밑각의 크기가 같다.2. 삼각형의 세 각의 합은 180도이다.만들어지는 임의의 두 삼각형의 한 밑각을 각각
다음과 같이 원의 중심에서 원 위의 임의의 한 점을 찍고 삼각형을 그어준다면,원의 중심에서 각 꼭지점까지의 거리는 반지름으로 동일하게 됩니다.이 그림에서 우리는 2가지의 특징만으로 90도임을 손쉽게 증명할 수 있습니다.1. 이등변삼각형의 정의 : 두 변의 길이가 같은 삼각형-> 특징 : 두 밑각의 크기가 같다.2. 삼각형의 세 각의 합은 180도이다.만들어지는 임의의 두 삼각형의 한 밑각을 각각라 정의한다면,
이 성립한단걸 알 수 있고,
결론적으로임을 알 수 있습니다.
그러므로 우리는 임의의 한 점의 각도가 어느 위치에든 상관없이 90도임을 증명할 수 있습니다.막상 하고보니 증명같지도 않고, 모두가 알고 있는 지식을 괜히 포장만 한거 같네요.