작년 추석때 철수에게 물었습니다.
자연수가 뭐니?
철수는 자신있게 대답 했습니다.
"1,2,3,4,5,6,7,8....... "
철수는 아직도 수를 말하고 있습니다.
"123423424234234,123423424234235, ....."
철수를 도와 주세요.^^
이런 방법은 어떨까요?
- 1 은 자연수이다.
- 어떤 수 n 이 자연수이면 n+1 도 자연수이다.
바로 보이는 쉬운 증명으로 가 보겠습니다.
(보기) 3 을 n 번 더하면 3n 이다. 이를 증명.
proof)
- n 이 1 일 때 3 이 성립
- n 일 때 성립한다고 하자. 즉
3+3+ ... + 3 = 3n ------- (1)
이 식을 이용해서 n+1 일 때 3(n+1) 가 됨을 보이면 됩니다.
1 식의 양변에 3 을 더하면
3+3+ ... + 3 + 3= 3n + 3 = 3(n+1) 증명 끝.
알쏭 달쏭 합니다. 맞는 증명보다는 거짓 명제 증명 으로 가보는게 이해가 더 쉬울 수도 있겠네요.
(보기) 3 을 n 번 더하면 2n+1 이다.
proof)
n 이 1 이면 3 을 만족
n 일 때 성립한다고 하자. 즉
3+3+ ... + 3 = 2n + 1 .............(1)
이를 이용해서 n+1 일 때 2(n+1) + 1 = 2n + 3 임을 보여야 합니다.
(1) 식의 양변에 3 을 더합니다.
3+3+ ... + 3 + 3 = 2n + 1 + 3 = 2n + 4
성립하지 않습니다.
수학적 귀납법으로 증명하는 방법은
1 일 때 성립 한다.
n 일 때 성립한다고 가정 한 후 이식을 이용해서 n+1 일 때 성립함을 보이는 증명 방법 입니다.
(문제) 1 + 3 + 5 + ... + 2n -1 =
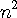
임을 수학적 귀납법으로 증명 하시요. (증명은 댓글로)
