We will describe two ways to approach the problem.
The "classic" approach is to develop the function f(N, S) = how many integers less than or equal to N
have the digit-sum S.
The solution is then f(B, S) − f(A−1, S).
To calculate the value of f, we use an auxiliary function g(len, S) = how many integers of length len
have the digit-sum S. The function g is easy to calculate using dynamic programming.
Suppose N is L digits long and its first digit is D.
Then f(N, S) = g(L−1, S) + g(L−1, S−1) + … +g(L−1, S−D+1) +
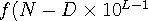
, S−D)
This can be calculated iteratively.
An alternative approach is to recursively build the number and take advantage of many subproblems
sharing the same solution. Suppose that, in our recursive function, we have decided on a prefix P of the
number. Then we know exactly what range of numbers can be built hereafter: if we put K more zeros,
we get
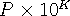
. If we put K nines, we get
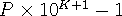
.
If this entire range is outside the interval [A, B], then we return 0. If the entire range is inside the
interval, then the solution is equivalent to calculating the function g from above (this is where many
subproblems share the same solution). If the range is partially inside [A, B], then we just continue the
recursion (try every digit). The key is to notice that this last case will happen only O(log B) times, so
this solution will be as efficient as the first one. The accompanying source code demonstrates the
second approach in a single function.
We can find the smallest integer with the digit-sum S while calculating the total number of integers.
An alternative is to use binary search to find the first number X such that the interval [A, X] contains
exactly one integer with the digit-sum S (this is equivalent to the first half of the problem).
, S−D)
This can be calculated iteratively.An alternative approach is to recursively build the number and take advantage of many subproblemssharing the same solution. Suppose that, in our recursive function, we have decided on a prefix P of thenumber. Then we know exactly what range of numbers can be built hereafter: if we put K more zeros,we get. If we put K nines, we get
.
If this entire range is outside the interval [A, B], then we return 0. If the entire range is inside theinterval, then the solution is equivalent to calculating the function g from above (this is where manysubproblems share the same solution). If the range is partially inside [A, B], then we just continue therecursion (try every digit). The key is to notice that this last case will happen only O(log B) times, sothis solution will be as efficient as the first one. The accompanying source code demonstrates thesecond approach in a single function.We can find the smallest integer with the digit-sum S while calculating the total number of integers.An alternative is to use binary search to find the first number X such that the interval [A, X] containsexactly one integer with the digit-sum S (this is equivalent to the first half of the problem).