[문제요약] 한 번에 게임을 끝내기 위한 최적의 방법(최소 이동)을 찾는 문제.

체커 게임

• 움직이는 방향: 대각선 + 로만 움직일 수 있고
• 공격: 대각선으로 적(o) 을 뛰어 넘은 후 공간(+)이 있으면 가능. 뛰어 넘킴을 당한 적(o)은 사라짐.

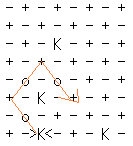
- + - + - + - +  K 는 베시의 왕: o 는 적
+ - + - + - + -  
- + - K - + - +  왕들은 연속적으로 적들의 checker 를 대각선 방향으로  넘을 수 있다.
+ - + - + - + -  넘김을 당한 적의 checker 는 죽는다.
- o - o - + - +
+ - K - + - + -  이 보드판의 답은 8 행 3 렬의 왕이 연속적으로 움직여 게임을 끝낼 수 있다.
- o - + - + - +  그림에서 움직이는 왕은 >K< 표시   
+ - K - + - K -  

입력의 데이터는 유일한 방법이 존재하거나 아니면 존재하지 않는다. 존재하지 않으면 impossible 을 출력

Given an NxN (4 <= N <= 30) checkboard, determine the optimal set of moves to end the game on the next move. Checkers move only on the '+' squares and capture by jumping 'over' an opponent's piece. The piece is removed as soon as it is jumped. See the example below where N=8:

- + - + - + - +  The K's mark Bessie's kings; the o's represent the
+ - + - + - + -  opponent's checkers. Bessie always moves next. The
- + - K - + - +  Kings jump opponent's checkers successively in any
+ - + - + - + -  diagonal direction (and removes pieces when jumped).
- o - o - + - +
+ - K - + - + -  For this board, the solution requires the lower left
- o - + - + - +  King to jump successively across all three of the
+ - K - + - K -  opponents' checkers, thus ending the game (moving K
                 marked as >K<):

   Original          After move 1       After move 2        After move 3
- + - + - + - +     - + - + - + - +    - + - + - + - +     - + - + - + - +
+ - + - + - + -     + - + - + - + -    + - + - + - + -     + - + - + - + -
- + - K - + - +     - + - K - + - +    - + - K - + - +     - + - K - + - +
+ - + - + - + -     + - + - + - + -    + ->K<- + - + -     + - + - + - + -
- o - o - + - +     - o - o - + - +    - + - o - + - +     - + - + - + - +
+ - K - + - + -    >K<- K - + - + -    + - K - + - + -     + - K ->K<- + -
- o - + - + - +     - + - + - + - +    - + - + - + - +     - + - + - + - +
+ ->K<- + - K -     + - + - + - K -    + - K - + - K -     + - K - + - K -

The moves traversed these squares:

  1 2 3 4 5 6 7 8           R C
1 - + - + - + - +    start: 8 3
2 + - + - + - + -    move:  6 1
3 - + - K - + - +    move:  4 3
4 + - * - + - + -    move:  6 5
5 - o - o - + - +
6 * - K - * - + - 
7 - o - + - + - + 
8 + - K - + - K - 

입력

• Line 1: A single integer: N
• Lines 2..N+1: Line i+1 contains N characters (each one of: '-', '+', 'K', or 'o') that represent row i of a proper checkboard.

출력

입출력 예

입력

8
-+-+-+-+
+-+-+-+-
-+-K-+-+
+-+-+-+-
-o-o-+-+
+-K-+-+-
-o-+-+-+
+-K-+-K-

출력

8 3
6 1
4 3
6 5

출처:usaco 2008 DEC bronze