2011 세계 올스타 테니스 대회를 준비중인 난쿤이는 보다 흥미진진한 게임을 진행하기 위해 특별한 토너먼트 대진표를 구성할 것을 제안하였다. 이 특별한 형태의 토너먼트 대진표란, 부전승을 임의로 선택해서라도 모든 게임에서 가급적 랭킹이 비슷한 사람끼리 대전을 하도록 대진표를 구성하는 것을 말한다.

(*상위 랭킹에 있는 사람이 상대적으로 이길 확률이 높기 때문에 대전하는 선수들 중 상위에 랭크되어 있는 사람이 무조건 게임에서 이긴다는 가정하에 토너먼트 대진표를 구성한다.) 일단 선수들을 추천에 의해서 번호를 뽑았으면, 각 번호 순서대로 게임이 진행되도록 대진표를 구성하도록 한다.

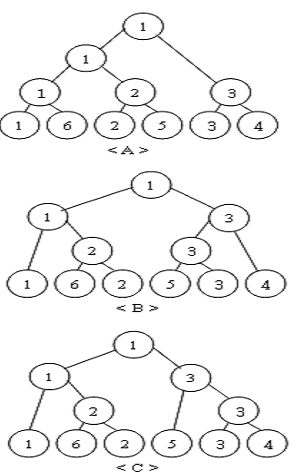
이 때, 토너먼트 게임 방식을 아래 그림에서 제시된 것들과 같이 여러 경우를 생각해 볼 수 있으므로 난쿤이는 보다 흥미진진한 게임이 진행되도록 이들 토너먼트 대진표에서 대전하게 될 상대 선수들의 랭킹의 차이의 총합이 최소가 되도록 대진표를 구성하려고 한다. 물론 입력순서대로 구성을 해야한다.

예를 들면 그림에서 원 안의 숫자가 선수의 랭킹이라고 할 때,  A 와 같은 토너먼트 대진표에서는<세계랭킹1위vs세계랭킹6위>,<2vs5>,<3vs5>,<1vs2>,<1vs3>와 각각 경기를 해서 대전할 때 선수들의 랭킹 차이의 합이 12가 되지만  B  같은 경우는 <6vs2>,<3vs4>,<1vs2>,<5vs3>,<1vs3> 의 경기를 치르게 되어 랭킹 차이의 총합이 10이하가 된다.

위와 같이 토너먼트 구성표를 어떻게 만드느냐에 따라 선수들의 랭킹 차이의 총 합이 달라지게 된다. 당신은 위에서 생각해 볼 수 있는 여러 토너먼트 대진표 중에서ㅓ, 선수들의 랭킹 차이의 총 합이 가장 작게 되었을 때의 랭킹 차이의 총합을 알려 주어야 하는 임무를 맡았다. 또한, 총 합이 가장 작은 경우가 여러 가지가 있을 경우에는 가능한 가짓수가 몇 가지가 있는지를 출력해야 한다.

입력

출력

입출력 예

입력

6
1 6 2 5 3 4

출력 

9
4

잘못된 데이터는 없다고 가정해도 좋다.

출처:algolab.org