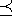 B (i.e., A "precedes" B), if
B (i.e., A "precedes" B), if
A rectangle in the Cartesian plane is speci ed by a pair of coordinates ( x1 , y 1) and (x2 , y2) indicating its lower-left and upper-right corners, respectively (where x1 <= x2 and y1 <= y2).
Given a pair of rectangles,
A = (( x1^A, y1^A) , ( x2^A ; y2^A)) and B = (( x1^B , y1^B) , ( x2^B ; y2^B)), we write
A 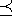 B (i.e., A "precedes" B), if
B (i.e., A "precedes" B), if
x2^A < x1^B and y2^A < y1^B .In this problem, you are given a collection of rectangles located in the two-dimension Euclidean plane.
Find the length L of the longest sequence of rectangles ( A1 , A2 , ..., AL) from this collection such that
A1 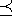 A2
A2 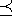 . . .
. . . 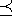 AL.
AL.
입력 3 1 5 2 8 3 -1 5 4 10 10 20 20 출력 2 입력 2 2 1 4 5 6 5 8 10 출력 1
출처:standford/2009/