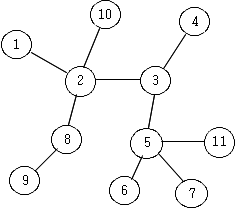
N개의 도시들과 이들 도시들을 연결하는 트리 형태의 도로망이 있다.

즉, 이 도로망은 임의의 두 도시 사이의 경로가 항상 하나만 있다. 다음은 11개의 도시들로 이루어진 트리 형태의 도로망의 예이다.

두 도시 u, v사이의 경로는 u로부터 인접한 도로들을 따라 v에 도달하는 길로서, 중간에 거치는 도시가 중복되어서는 안 된다.

이 경로는 u부터 시작하여 지나는 도시들을 순서대로 나열하여 나타낸다.

예를 들어, 9부터 10까지의 경로는 (9, 8, 2, 10)으로 나타낸다.

양의 정수 K에 대하여, 이 트리 형태의 도로망의 K-경로 분할은 다음 조건을 만족하는 경로들의 집합이다.

• 이들 경로들 중 임의의 두 경로가 같은 도시를 지나서는 안 된다,
• 도로망의 각 도시는 반드시 이들 경로 중 하나에 포함되어야 한다.
• 각 경로는 길이가 K 이하이어야 한다. 경로의 길이란, 이 경로 상에 있는 도로(간선)의 개수이다.

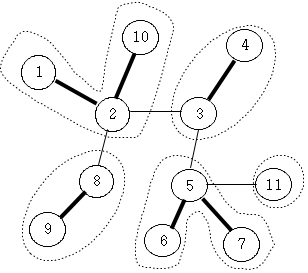
예를 들어, 위 그림에 있는 도로망의 2-경로 분할 중 하나는 다음과 같다.

{(1, 2, 10), (8, 9), (3, 4), (6, 5, 7), (11)}

이 2-경로 분할에 있는 경로들은 아래 그림에서 점선 부분으로 표시되어 있으며, 경로들의 개수가 5이다.

이는 경로들의 수가 최소인 2-경로 분할 중 하나이다.

또 다른 예로, 다음은 3-경로 분할 중 하나이다.

{(1, 2, 3, 4), (8, 9), (10), (6, 5, 11), (7)}

이 분할에서 경로 개수는 5로서 3-경로 분할 중 경로 수가 가장 작다.

또 다른 예로, 다음은 1-경로 분할 중 하나이다.

{(1, 2), (10), (8, 9), (3, 4), (5, 6), (11), (7)}

이 분할에서 경로 개수는 7로서 1-경로 분할 중 경로 수가 가장 작다.

트리 형태의 도로망과 K가 주어질 때, 경로 개수가 가장 작은 K-경로 분할의 경로 수를 구하는 프로그램을 작성하시오.

실행시간은 1초를 넘을 수 없으며, 부분 점수는 없다.

입력 형식

• 첫째 줄에는 도시의 수 N과 K-경로 분할을 위한 수 K가 빈칸을 사이에 두고 입력된다. N은 2 이상 300,000이하, K는 1이상 N-1이하인 정수이다.
• 다음 N-1개의 각 줄에 도로의 양 끝 도시를 나타내는 두 정수가 빈칸을 사이에 두고 주어진다.

출력 형식

경로 개수가 가장 작은 K-경로 분할의 경로 수를 출력한다.

제약 조건

• K = 1인 경우는 전체 테스터 데이터의 20%이다.
• K > 1이고, N이 1000이하인 경우는 전체 테스터 데이터의 30%이다.

입력과 출력의 예

입력 

11 2
1 2
2 10
2 3
3 4
3 5
5 11
5 7
6 5
2 8
8 9

출력

5

출처:koi 2011 전국본선 고등부 3번
문제작업:tncks0121