N개의 꼭지점을 갖는 볼록다각형 모양의 KOI랜드에는 각 꼭지점에 도시가 건설되어 있으며 모든 도시는 볼록다각형의 각 변으로 구성된 일주도로로 연결되어 있다. 한 도시에서 다른 도시로 가려면 일주도로를 이용하여야 한다. 특정 두 도시를 연결하는 하나의 직선인 횡단도로를 건설하여 모든 도시들 사이의 최단 경로 가운데 길이가 가장 긴 것을 최소화하려고 한다.

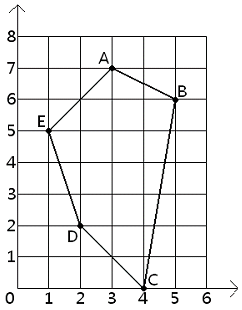
예를 들어, 아래 그림과 같이 5개 도시와 일주 도로가 건설되어 있을 경우, 도시 A와 C 사이의 최단 경로 (A↔B↔C)의 길이가 √5 + √37 로 가장 길다.

도시 B와 E 또는 C와 E 또는 B와 D를 횡단도로로 연결하면 가장 긴 최단경로에 변화가 없다. 도시 A와 C를 횡단도로로 연결하면 도시 B와 D 사이의 최단경로 (B↔A↔E↔D)의 길이가 √5 + √8 + √10 로 가장 길게 된다.

또한 도시 A와 D를 횡단도로로 연결하면 도시 A와 C 사이의 최단경로 (A↔D↔C)의 길이가 √26 + √8 로 가장 길게 된다. √26 + √8 < √5 + √8 + √10 < √5 + √37 이므로, 도시 A와 D를 횡단도로로 연결하면 모든 도시들 사이의 최단 경로 가운데 가장 긴 것이 최소가 된다.

N개 도시의 위치가 주어졌을 때, 모든 도시들 사이의 최단경로 가운데 가장 긴 것의 길이를 최소화하기 위하여 횡단도로로 연결해야 하는 두 도시를 결정하는 프로그램을 작성하라.

입력

• 첫째 줄에 도시의 개수 N (4 ≤ N ≤ 300)이 주어진다.
• N개 도시의 위치가 시계방향의 순서로 둘째 줄부터 한 줄에 하나씩 주어진다. 각 도시의 위치는 평면상의 좌표 (X, Y)로 주어진다. X와 Y는 0 이상 200,000 이하인 정수다.

출력

입출력 예

입력

5
3 7
5 6
4 0
2 2
1 5

출력

3 7 2 2

출처: 2009 koi 지역 중등 4 번

* 아직 스페셜저지 처리를 하지 않았습니다.