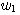 과
과 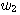 가 있다고 하자.
가 있다고 하자.길이가 같은 두 개의 이진수 코드 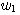 과
과 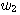 가 있다고 하자.
가 있다고 하자.
이 두 코드 사이의 해밍 거리(Hamming distance)는 의 각 비트를 왼쪽부터 오른쪽으로 차례대로 비교할 때 서로 다른 값을 가진 비트의 수이다.
예를 들어, 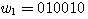 ,
, 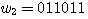 이라고 하면, 세 번째 비트와 여섯 번째 비트만 서로 다르므로 해밍 거리는 2이다
이라고 하면, 세 번째 비트와 여섯 번째 비트만 서로 다르므로 해밍 거리는 2이다
KOI 연구소는 특정 암호문에서 사용되는 총 N개의 이진 코드를 가지고 있다. 각 코드의 길이는 K로 일정하다. 연구소는 이 코드들에 대해 여러 가지 특징을 분석하고 있다.
예를 들어, 다음과 같이 길이가 3인 5개의 이진 코드들이 있다고 하자.
|
|
|
|
|
|
|
|
|
|
두 코드 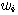 와
와 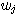 사이의 해밍 거리를
사이의 해밍 거리를 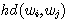 로 표현한다.
로 표현한다.
그러면, hd(w1,w2) = 3, hd(w1,w3) = 1, hd(w1,w4) = 2, hd(w1,w5) = 1
당신은 이진 코드들에 대해 해밍 경로를 찾고자 한다. 해밍 경로는 모든 인접한 두 코드사이의 해밍 거리가 1인 경로이다. 위의 예에서 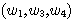 는 길이가 3인 해밍 경로이지만,
는 길이가 3인 해밍 경로이지만, 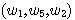 는 해밍 경로가 아니다. 두 코드 사이에 해밍 경로가 여러 개가 있을 경우 가장 짧은 경로를 찾고자 한다
는 해밍 경로가 아니다. 두 코드 사이에 해밍 경로가 여러 개가 있을 경우 가장 짧은 경로를 찾고자 한다
이 문제는 1번 코드에서부터 질의로 주어진 여러 개의 코드까지의 해밍 경로를 각각 구하는 프로그램을 작성하는 것이다. 프로그램의 실행시간은 2초를 넘을 수 없다.
출력은 M개의 줄로 구성된다.각 줄에는 입력으로 주어진 각 질의에 대한 답을 순서대로 출력한다.
만일 두 코드 사이에 해밍 경로가 존재하면 가장 짧은 경로에 있는 코드들의 번호를 1번 코드부터 차레로 하나의 빈칸을 사이에 두고 출력한다. 답이 여러 개 있으면 그 중에 하나만 출력하고, 경로가 존재하지 않으면 -1을 출력한다.
입력 5 3 000 111 010 110 001 2 4 2 출력 1 3 4 1 3 4 2
출처 : KOI 2010 지역본선 3번 special judge: Fate 참고 : http://183.106.113.109/pool/hamming_distance/hamming_distance.php?pname=hamming_distance