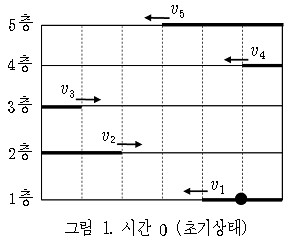
여러 층으로 이루어진 직사각형 모양의 건물이 있다. 아래 그림 1은 5개의 층으로 이루어진 직사각형 건물의 예이다. 각 층에는 하나의 막대기가 있는데, 각 막대기의 길이는 서로 다를 수 있다. 그리고 막대기들은 시간 0 에서 시작해서 동시에 각각 일정한 속도로 왼쪽에서 오른쪽으로 혹은 오른쪽에서 왼쪽으로 움직인다. 각 막대기의 움직이는 속도는 양의 정수로 주어진다.

그림 1에서처럼 초기(시간 0)에 각 막대기는 직사각형의 왼쪽 변 또는 오른쪽 변에 닿아있다. 시간이 지남에 따라 각 막대기는 주어진 방향으로 주어진 속도로 움직이고 막대기의 양쪽 끝 중에 하나가 직사각형의 왼쪽 변 또는 오른쪽 변에 닿으면 진행하는 방향과 반대 방향으로 계속해서 움직인다.

철수(그림 1의 검정색 원)는 초기에 가장 아래층막대기 위에 위치하고 있다. 그리고 아래 조건 1)을 만족하면서 현재 막대기 위에서 움직일 수 있고, 조건 2)를 만족한다면, 위층에 있는 막대기 중 하나로 올라 갈 수 있다.

• 조건 1) 현재 위치하고 있는 막대기 위에서는 0 시간에 움직일 수 있다. (즉, 막대기 위에서의 움직임은 시간이 걸리지 않는다.)
• 조건 2) 주어진 정수 K ( 1 <= K <= N-1) 에 대해서, 철수가 현재 위치하고 있는 막대기 위의 임의의 위치가 현재 층에서 최대 K 개 위의 어떤 층의 막대기 구간 안에 있게 되면(구간의 양쪽 끝 포함) 0 시간에 그 층의 막대기로 수직으로 올라갈 수 있다. (즉, 이 조건을 만족해서 위 층으로 올라 갈 수 있다면, 올라가는 움직임은 시간이 걸리지 않는다.)

시간 0 의 초기 상태에서 출발해서 철수가 가장 아래층의 막대기에서 가장 위층의 막대기로 올라가는데 걸리는 최소 시간을 구하는 프로그램을 작성하시오.

입력

• 첫 번째 줄에 층 수 N ( 1 <= N <= 1000) , 층의 길이 L ( 1 <= L = 3000) 과 조건 2)에서 주어진 정수 K( 1 <= K <= N-1) 가 주어진다. 가장 아래층은 1 층이고 가장 위층은 N 층이다.
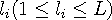• 다음 N 개의 줄 중 i 번째 줄에는 i 층의 막대기의 길이 , 초기에 막대기가 움직이는 방향 di(di =0,1)와 막대기의 움직이는 속도 vi ( 1 <= vi <= L)가 주어진다. 여기서, 속도 vi는 정수로 주어지고, di의 값 0 은 왼쪽에서 오른쪽, 1 은 오른쪽에서 왼쪽을 의미한다. 또한 초기에 막대기들은 방향이 0 인 경우 층의 왼쪽 벽에, 1 인 경우 층의 오른쪽 벽에 닿아 있다고 가정한다.

출력

입출력 예

입력

5 7 2
2 1 1
1 0 1
3 1 1
1 1 1
4 0 1

출력 

0.00000

입력 

5 7 2
1 1 2
1 0 4
2 1 3
1 1 2
4 0 1

출력 

0.25000

출처:2012 지역 본선 고등 4/5