이 문제는 톨게이트(koi_gate) 문제의 작은 확장입니다.
어느 나라에는 N 개의 도시와 M개의 도로로 구성된 도로망이 있다. 각 도로는 서로 다른 두 도시를 직접 잇는 형태이며, 서로 다른 두 도로가 도로의 중간에서 교차하는 일은 없다. 도로는 양 방향 통행이 가능하고, 한 쌍의 도시 사이에는 최대 하나의 도로가 있다. 모든 개별 도로들의 길이 는 동일하다. 또한, 도로망을 통해서 어떤 도시에 서든 다른 모든 도시로 이동이 가능하다. 모든 도 시의 인구수는 1 이상의 자연수이다. 각 도시에는 0개 이상의 맛집이 있다. (맛집은 유명한 음식점을 말한다.)
이 나라의 도로망을 조사해 보니 특이한 점을 한 가지 발견하게 되었다. 처음과 끝 도시가 같고 나머지 도시들은 서로 다른 경로를 단순 사이클(simple cycle)이라고 부른다. 이 나라의 도로망의 특이한 점은 모든 개별 도로는 최대 하나의 단순 사이클에 속한다는 것이다.
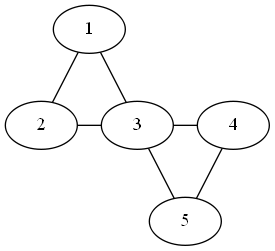
아래 그림은 3번 도시가 두 개의 단순 사이클에 포함되어 있지만, 모든 도로가 하나의 단순 사이클에 포함되므로 문제에서 주어질 수 있는 경우이다.

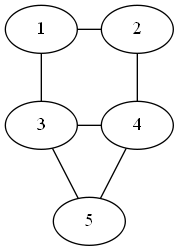
아래 그림은 불가능한 경우이다. 3과 4를 잇는 도로가 두 개의 단순 사이클에 포함되기 때문이다.
이 나라의 모든 사람들은 일 년 동안 모든 맛집을 한 번씩만 다녀온다. A 도시에 사는 사람이 B 도 시의 맛집을 다녀온다는 것은 A에서 출발하여 B 에 있는 하나의 맛집만 방문하고 A로 다시 돌아 오는 것을 말한다. (즉, 그 과정에서 다른 맛집을 방문하지 않는다.) 또, A에서 B의 맛집을 다녀오는 경우 A에서 B로 가는 가장 짧은 길을 왕복한다. 가장 짧은 길이 여러 개 존재하는 경우는 동일한 확률로 그 중 하나를 선택한다. 이 나라의 재정이 최근 부족하여 도로들 중 단 하나에 톨게이트를 설치하려고 한다. 톨게이트를 어느 방향으로 통과하든 비용을 지불해야 하며 이동 거리에 관계없이 모두 동일한 비용을 지불한다.
도시의 수, 도시별 인구수와 맛집의 수, 그리고 도로망을 입력 받아 일 년 동안 가장 많은 통행료 수입을 기대할 수 있는 도로를 찾는 프로그램을 작성하라. 동일한 기댓값을 가지는 도로가 여러 개인 경우 모두 다 출력하여야 한다.
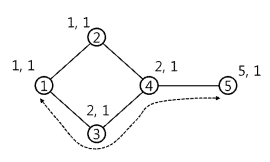
아래 그림의 예를 보자.
그림에서 원 안에 있는 수는 도시의 번호이며, 원 옆에 있는 두 수는 각 각 도시의 인구수와 맛집의 수이다. 화살표는 1번 도시와 5번 도시 간의 가장 짧은 길의 한 예이다. 1번 도시에서 2번 도시로 가는 가장 짧은 길은 한 가지 뿐이지만, 1번 도시에서 5번 도시로 가는 가장 짧은 길은 두 가지이다. 모든 상황을 고려하면 4번 도시와 5번 도시 사이에 톨게이트를 설치 하는 것이 가장 많은 통행료 수입을 기대할 수 있음을 알 수 있다.
수행 시간은 2초를 넘을 수 없다. 부분점수는 없다.
입력 5 4 1 1 1 1 1 1 1 1 1 1 1 2 2 3 3 4 4 5 출력 2 2 3 3 4 입력 5 5 1 1 1 1 2 1 2 1 5 1 1 2 1 3 2 4 3 4 4 5 출력 1 4 5 입력 5 6 1 1 1 2 1 1 1 2 1 1 1 2 1 3 1 4 1 5 2 3 4 5 출력 2 1 2 1 4
출처:zlzmsrhak + Fate