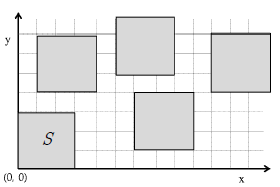
연꽃잎들이 떠있는 풍경으로 유명한 연못이 있다. 이 연못에 살고 있는 개구리는 연꽃잎과 연꽃잎 사이를 점프해서 움직이기를 좋아한다.

연못은 x,y 좌표로 표현되는 평면 상에서 x≥0, y≥0인 구역 R로 나타낸다. 연못에 떠 있는 연꽃잎은 구역 R 안에서 한 변의 길이가 r 인 정사각형으로 나타낸다 (그림 1). 모든 연꽃잎 의 크기는 동일하고 서로 겹치지 않는다고 가정한 다. 임의의 두 연꽃잎들의 테두리가 맞닿아 있는 경우는 없다.

좌표 (0,0) 을 포함하는 연꽃잎 S 는 항상 존재하고 개구리는 처음에 이 연꽃잎 위에 놓여있다.

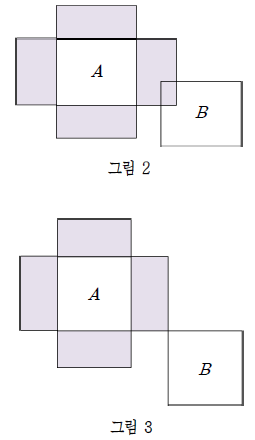
개구리는 한 번의 점프로 최대 거리 d 만큼 이동 할 수 있다. 다만, 동, 서, 남, 북 방향으로만 점프 할 수 있다. 따라서 개구리가 그림 2, 3의 연꽃잎 A 에서 점프한다면 도달할 수 있는 영역은 그림 2, 3의 어두운 구역과 같다. 개구리가 연꽃잎 A 에서 다른 연꽃잎 B로 점프하기 위해서는 그림 2 에서와 같이 이 구역 안에 B 의 일부분이 놓여 있어야 한다. 그림 3과 같이 이 구역에 B의 테두리가 닿아 있는 경우도 점프할 수 있다고 가정한다.

개구리가 처음 시작 연꽃잎 S 에 놓여 있을 때, 연꽃잎 위에서 이동하거나 연꽃잎에서 연꽃잎으로 점프해서 어떤 연꽃잎 위의 좌표 (a,b)인 위치로 이동 할 수 있다. 문제는 (0,0)으로부터 이동 가능한 가장 먼 좌표 (a,b)를 찾는 것이다. 여기서, 좌표 (a,b)의 (0,0)으로부터의 거리는 a+b 로 계산된다.

수행 시간은 1초를 넘을 수 없다. 부분점수는 없다.

입력

• 첫째 줄에 두 개의 정수 N,r 이 주어진다. 단, 그 범위는 1 ≤ N ≤100 000 , 1 ≤ r ≤10 000 이다. 여기서, N 은 연꽃잎들의 수를 나타내고 r은 연꽃잎 의 한 변의 길이를 나타낸다.
• 다음 N 개의 줄 각 각에는 하나의 연꽃잎의 왼쪽 아래 꼭지 점의 좌표 (x,y)를 나타내는 두 정수 x 와 y가 공백을 사이에 두고 주어진다. 단, 0 ≤ x,y ≤ 10 000 000이다.
• 다음 줄에는 개구리가 한 번의 점프로 연꽃잎 사이를 이동할 수 있는 최대 거리 d 가 주어 진다. 단, 1 ≤ d ≤1 000 000 이다.

출력

입출력 예

입력

5 3
0 0
1 4
5 5
6 1
10 4
1

출력

20

입력

12 3
0 0
4 0
9 0
17 0
13 2
2 5
7 5
19 6
3 9
9 9
15 9
19 10
2

출력

24

출처:2013 koi 중등지역본선 3/5