2차원 좌표평면상에 x-축과 평행한 서로 다른 두 직선 L1, L2와 이 두 직선을 연결하는 선분들이 있다. 이 문제에서는 다음 조건을 만족시키는 선분들의 집합을 고려한다.

1. 선분들의 끝점들은 서로 겹치지 않는다.
2. 선분들은 각 집합 안에 있는 어떤 두 선분도 서로 교차되지 않도록 두 개의 집합 X와 Y로 분할될 수 있다.

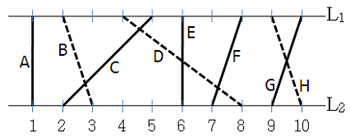
아래 그림은 위 조건을 만족시키는 선분 집합의 한 예이다. 두 번째 조건의 경우, 선분들을 X={A, C, E, F, G}(실선 표시)와 Y={B, D, H}(점선 표시)로 분할하면 같은 집합 안의 어떤 두 선분도 교차되지 않음을 알 수 있다.

선분 집합에서 일부 선분들을 뽑아 선분들의 리스트 (s1,s2,..,sk)를 구성할 수 있는데, 리스트 상에서 모든 인접한 두 선분 si 와 si+1 (1 <= i < k)이 서로 교차하면, 이 리스트를 선분 체인(chain)이라 부른다. 선분 체인의 길이는 체인을 구성하는 선분들의 개수로 정의된다. 예를 들어, 위 그림에서 선분 리스트 (B, C, D, F)는 길이가 4인 선분 체인이지만, (A, C, D)는 선분 체인이 아니다.

위의 조건을 만족하는 선분들의 집합이 주어졌을 때, 이 집합으로부터 만들 수 있는 가장 긴 선분 체인의 길이를 구하는 프로그램을 작성하시오.

입력

• 첫째 줄에는 선분의 개수 N이 입력된다. N은 1이상 100,000 이하이다.
• 둘째 줄부터 N개의 줄에 한 줄에 하나씩 선분에 대한 정보가 입력된다. 선분에 대한 정보는 L1상에 놓인 끝점의 x-좌표값과 L2상에 놓인 끝점의 x-좌표값이 순서대로 주어진다. 좌표값은 모두 1이상 1,000,000 이하인 정수이다.

출력

입출력 예

입력

8
1 1
2 3
5 2
4 8
6 6
8 7
10 9
9 10

출력

4

출처:koi 2010 고등 3 번