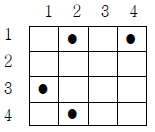
행의 크기와 열의 크기가 각각 N 인 격자공간에 M 개의 점이 있다. N = 4이고M = 4 인 경우의 예가 아래에 있다. 격자공간 왼쪽의 숫자는 행 번 호이며, 위의 숫자는 열 번호를 나타낸다. 그리고 격자공간내의 각 사각형의 위치는 (행 번호, 열 번호)로 표시한다.

이제 격자공간에 있는 모든 점들을 하나의 사각형 안으로 모으려고 한다. 어떤 점을 움직일 때는 그 점이 들어있는 사각형에서 상하좌우로 인접한 사각형으로만 움직일 수 있다. 여기에서는 격자공간내의 한 사각형으로 모든 점 들을 모을 때 각 점이 움직인 거리의 합을 고려한다.

예를 들어, 위의 점들을 (3,2)에 있는 사각형으로 모을 때 최단거리로 점들을 이동시킨다면 (1,2)에 있는 점의 이동거리는 2이고, (3,1)과 (4,2)에 있는 점의 이동거리는 각각 1 이며, (1,4) 에 있는 점의 이동거리는 4 이므로 점들이 움직인 거리의 합은 8이다. 또, 위의 모든 점들을 (1,2)의 위치로 모을 때도 점들이 이동한 거리의 합이 8 임을 알 수 있다. 위의 예에서는 점들을 어떤 하나의 사각형으로 모을 때 이동거리의 합이 8보다 작게 되는 사각형은 없다.

이 문제는 주어진 격자공간에 있는 모든 점들을 하나의 사각형으로 모을 때 드는 이동거리의 합의 최솟값을 구하는 것이다. 주어진 격자공간에서는 하나의 사각형에 여러 개의 점들이 들어 있을 수 도 있고, 점들을 모을 때는 어떤 점이 들어 있는 사각형으로도 모을 수 있다고 가정한다.

수행 시간은 1 초를 넘을 수 없으며 부분점수는 없다.

입력

• 첫 줄에는 격자공간의 크기와 점들의 개수를 나타내는 두 정수 N 과 M 이 하나의 공백을 사이에 두고 주어진다.
• 다음의 M 줄에는 각 줄마다 격자공간내의 점 의 위치를 나타내는 두 개의 정수가 하나의 공백을 사이에 두고 주어진다. 단, N 의 크기는 1이상 10,000이하이고, M 의 크기는 1 이상 100,000 이하이다.

출력

입출력 예

입력

4 4
1 2
1 4
3 1
4 2

출력 

8

출처:2013 koi 초등지역 본선 5/5