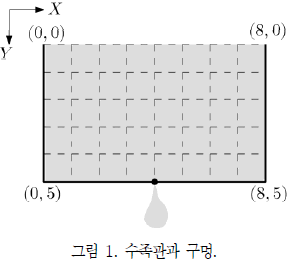
아래 그림 1은 수족관을 앞에서 본 모양이다. 이 수족관에는 물이 가득 차 있다. 만약 수족관 밑바닥(수평선분)에 구멍을 하나 뚫으면, 구멍을 통해 수족관 안의 물이 빠지게 된다.

그림 1에서 보는 것처럼, X-축은 왼쪽에서 오른쪽으로 증가하고, Y-축은 위쪽에서 아래쪽으로 증가한다. 바닥을 나타내는 수평선분에 구멍이 있 다면, 그 수평선분의 .-좌표와 같거나 작은 위치에 있으면서, 중력에 따라 구멍으로 흘러 들어갈 수 있는 위치에 있는 물은 모두 그 구멍을 통해 외부로 배출된다. 따라서 그림 1의 수족관의 물은 바닥의 구멍을 통해 남김없이 모두 빠진다.
수족관에 담긴 물의 양은 물이 차지하는 면적과 일치하는 양이다. 물의 양의 단위는 L(리터)이다. 따라서 그림 1에서 수족관에 물을 가득 채우면 물의 양은 물이 차지하는 면적과 동일한 40L이 다.
하나의 구멍을 통해 1초당 1L의 물이 빠져나간다고 하자. 그러면, 그림 1의 경우에는 40초만에 물 이 모두 빠진다.
그림 2처럼 수족관의 바닥이 복잡할 수도 있다
수족관 바닥은 수평선분과 수직선분이 번갈아 나타나는 형태이다. 또한 아래 그림 2처럼 수족관 위에서 수직방향으로 수족관 바닥을 보았을 때, 수족관의 바닥이 모두 보이는 (즉, 모든 수평선분이 보이는) 형태이다.
수족관에는 하나 이상의 구멍이 존재하는데, 구멍은 수평선분에만 존재하며, 수평선분의 한 가운데 에만 위치한다. 그리고 하나의 수평선분에는 최대 하나의 구멍만 존재할 수 있다.
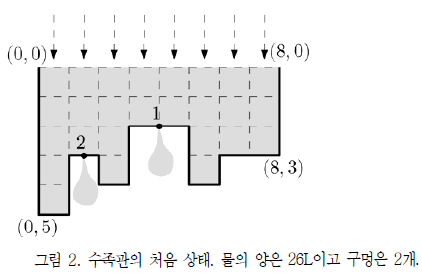
그림 2에는 2개의 수평선분에 총 2개의 구멍(1번 구멍과 2번 구멍)이 뚫려 있다. 처음 물의 양은 26L이다. 2개의 구멍을 통해, 0초부터 물을 빼기 시작하면 몇 초 후부터 더 이상 물이 빠지지 않게 될까?
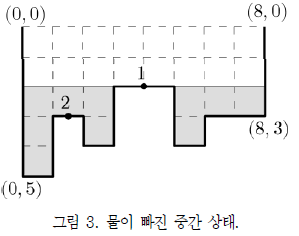
우선, 1번 구멍이 놓인 수평선분의 위쪽 부분에 있는 물 16L가 1번 구멍과 2번 구멍을 통해 동시 에 빠져 나가게 된다. 16L가 두 개의 구멍을 통 해 배출되므로, 8초 후에는 그림 3과 같은 상태가 된다.
이후에는 3L의 물이 2번 구멍을 통해 3초 동안 배출된다. 결국, 8초+3초 = 11초 동안 물이 배출 되고, 그 이후에는 더 이상 배출되지 않는다. 11 초 후에 남은 물의 양은 7L이며, 최종 상태는 그 림 4와 같다.
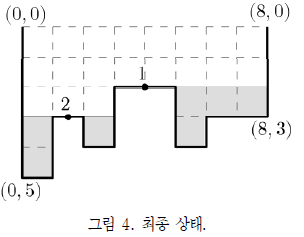
물이 가득 찬 수족관 바닥의 모양과 구멍이 뚫려 있는 수평선분들이 입력으로 주어지면, 물이 빠지는 데 걸리는 시간(초)과 남은 물의 양을 계산하 는 프로그램을 작성하시오.
수행시간은 1초를 넘을 수 없다.
입력 4 0 0 0 5 8 5 8 0 1 0 5 8 5 출력 40.00 0 입력 14 0 0 0 5 1 5 1 3 2 3 2 4 3 4 3 2 5 2 5 4 6 4 6 3 8 3 8 0 2 1 3 2 3 3 2 5 2 출력 11.00 7
출처:koi 30 회(2013 8 2) 전국 본선 중등부 문제 4/4대회 풀이