가로 길이가 w이고 세로 길이가 h인 2차원 격자 공간이 있다. 이 격자는 아래 그림처럼 왼쪽 아래 가 (0,0) 이고 오른쪽 위가 (w,h) 이다. 이 공간 안의 좌표 (p,q)에 개미 한 마리가 놓여있다.
개미는 오른쪽 위 45 도 방향으로 일정한 속력으로 움직이기 시작한다. 처음에 (p,q)에서 출발한 개미는 1시간 후에는 (p+1,q+1) 로 옮겨간다. 단, 이 속력으로 움직이다가 경계면에 부딪치면 같은 속력으로 반사되어 움직인다.

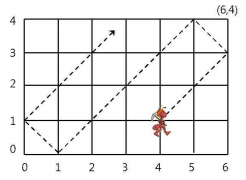
위 그림은 6×4 격자에서 처음에 (4,1)에서 출발한 개미가 움직인 길을 보여주고 있다. 처음에 (4,1) 에 있는 개미는 2시간 후에 (6,3)에 있으며 8시간 후에 (0,1)에 있다. 만일 그 개미가 처음에 (5,3)에 있었다면 매 시간마다 (6,4),(5,3),(4,2),(3,1)로 움직인다.
여러분은 크기 w×h인 격자 공간에서 처음에 (p,q)서 출발하는 개미의 t시간 후의 위치 (x,y)를 계산하여 출력해야 한다. 개미는 절대 지치지 않고 같은 속력으로 이동한다고 가정한다.
문제에서 w와 h는 자연수이며 범위는 2 ≤w,h ≤ 40,000이다. 그리고 개미의 초기 위치 p와 q도 자연수이며 범위는 각각 0 < p < w 과 0 < q < h이다. 그리고 계산할 시간 t의 범위는 1 ≤ t ≤ 2,000,000,000이다.
단, 채점 데이터의 40%는 1 ≤t ≤ 100,000,000이다.
수행 시간은 1초를 넘을 수 없다.
입력 6 4 4 1 8 출력 0 1 입력 6 4 5 3 4 출력 3 1
출처: 제31회 한국정보올림피아드 시/도 지역 본선 (2014.5.24) 초등부 문제 3,중등 2 채점데이터:Fate대회 풀이