프로그램 명: ioi_rings
제한시간: 3 초
오래전 잘 설계된 낙하산은 Leonardo's Codex Atlanticus 에 의해서 고안되었다.
레오나드의 낙하산은 린덴천으로 이루어져 있고 피라미드 모양의 나무 구조로...
이어진 링
스카이다이버 아드리안 니콜라스는 레오나드의 다자인을 테스트 했다.
현재의 가벼운 구조는 레오나드의 낙하산을 인체에 묶었다.
우리는 링크드된 링을 사용하기를 원한다. 또는 훅은 제공한다 실드된 린넨 천으로.
링은 유연하고 강한 물질로 만들어진다.
링은 쉽게 이어질 수 있다. 모든 링이 펼쳐질수 있고 다시 접을수 있게.
이어진 일련의 특별한 특징은 체인이다.
체인은 일련의 링인데 각 링은 많아야 두개의 이웃링으로 연결되어야 한다 그림처럼.
이 나열은 시작과 끝을 가지고( 많아야 하나의 다른 링으로 연결)
특별히 하나의 링도 또한 체인이다.

다른 구조도 확실히 가능하다. 왜냐하면 링은 세 개이상의 다른 링과 연결될 수 있다.
우리는 말한다. 링은 중요하다. 그것을 열고 제거한 후에 ,
모든 다른 링은 체인의 집합으로 이루어져 있다.(혹은 남겨진 다른 링이 없다). 다시말하면 ....
예
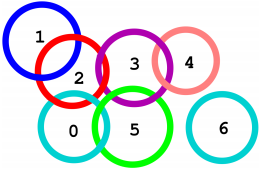
다음 그림에서는 7 개의 링이 있다. 0 에서 6 까지 번호가 붙은.
두개의 중요한 링이 있다.
하나의 중요한 링은 2 :
이 것을 제거하면 다른 링은 3 개의 체인 [1], [0, 5, 3, 4] , [6] 로 나뉜다.
다른 중요한 링은 3:
이 것을 제거하면 세 개의 체인이 생긴다.[1, 2, 0, 5], [4] and [6].
우리는 다른 링을 제거한다면 , 우리는 분리된 다른 체인을 얻을 수 없다.
예를 들어 5 번 링을 제거한 후:
[6] 은 체인이지만 이어진 링은 0, 1, 2, 3 and 4 은 체인을 이루지 못한다.
문제
당신이 해야 할 일은 주어진 구조에서 중요한 링의 수를 찾는 것이다.
처음 , 분리된 링이 있다.
다음으로 링을 연결 시킨다.
어떤 시점에 당신은 현재 구조에서 중요한 링의 수를 구하라는 명령을 받는다.
- Init(N) -
최초 한 번 불려진다. 분리된 N 개의 링이 주어진다. 각각은 0 에서 N-1 의 번호를 가진다.
-
Link(A, B) -
A , B 일을 연결 한다.
보장된다. A 와 B 는 다르고 이미 링크되지 않았다..
이거와 별개로 , A 와 B 에는 다른 조건이 없다.
특별히 물리적인 제약으로 부터 일어나는 어떤조건도 없다.
Link(A,B) 와 LINK(B,A) 는 같다.
-
CountCritical() -
현재 상태에서 중요한 일의 개수를 출력한다.
입력
-
첫 줄에 N 과 n 이 주어진다.
-
다음 n 개의 줄에는 연결된 두 개의 링 번호 혹은 -1 이 주어진다.
출력
입력값이 -1 이면 현재 상태에서의 중요한 링의 개수를 출력한다.
입출력 예
입력
7 13
-1
1 2
-1
0 5
-1
2 0
-1
3 2
-1
3 5
-1
4 3
-1
출력
7
7
7
7
4
3
2
▒ 대회 소스로 case 별 가장 긴 시간이 1.90 초 정도가 나와서 제한시간 3 초로 두었습니다.
An early and quite sophisticated version of what we now call a parachute is described in
Leonardo's Codex Atlanticus (ca. 1485). Leonardo's parachute consisted of a sealed linen cloth held
open by a pyramid-shaped wooden structure.
Linked rings
Skydiver Adrian Nicholas tested Leonardo's design more than 500 years later. For this, a modern
lightweight structure tied Leonardo's parachute to the human body. We want to use linked rings,
which also provide hooks for the sealed linen cloth. Each ring is made of flexible and strong
material. Rings can be easily linked together as every ring can be opened and re-closed. A special
configuration of linked rings is the chain. A chain is a sequence of rings in which each ring is only
connected to its (at most two) neighbours, as illustrated below. This sequence must have a start and
an end (rings that are connected to at most one other ring each). Specifically, a single ring is also a
chain.
 Other configurations are clearly possible, since a ring can be linked to three or more other rings. We
say that a ring is critical if after opening and removing it, all remaining rings form a set of chains (or
there are no other rings left). In other words, there can be nothing but chains left.
Example
Consider the 7 rings in the next figure, numbered from 0 to 6. There are two critical rings. One
critical ring is 2: after its removal, the remaining rings form chains [1], [0, 5, 3, 4] and [6]. The other
critical ring is 3: after its removal, the remaining rings form chains [1, 2, 0, 5], [4] and [6]. If we
remove any other ring, we do not obtain a set of disjoint chains. For example, after removing ring
5: although we have that [6] is a chain, the linked rings 0, 1, 2, 3 and 4 do not form a chain.
Other configurations are clearly possible, since a ring can be linked to three or more other rings. We
say that a ring is critical if after opening and removing it, all remaining rings form a set of chains (or
there are no other rings left). In other words, there can be nothing but chains left.
Example
Consider the 7 rings in the next figure, numbered from 0 to 6. There are two critical rings. One
critical ring is 2: after its removal, the remaining rings form chains [1], [0, 5, 3, 4] and [6]. The other
critical ring is 3: after its removal, the remaining rings form chains [1, 2, 0, 5], [4] and [6]. If we
remove any other ring, we do not obtain a set of disjoint chains. For example, after removing ring
5: although we have that [6] is a chain, the linked rings 0, 1, 2, 3 and 4 do not form a chain.

Statement
Your task is to count the number of critical rings in a given configuration that will be
communicated to your program.
At the beginning, there are a certain number of disjoint rings. After that, rings are linked together.
At any given time, you can be asked to return the number of critical rings in the current
configuration. Specifically, you have to implement three routines.
- Init(N) - it is called exactly once at the beginning to communicate that there are N
disjoint rings numbered from 0 to N - 1 (inclusive) in the initial configuration.
-
Link(A, B) - the two rings numbered A and B get linked together. It is guaranteed that A
and B are different and not already linked directly; apart from this, there are no additional
conditions on A and B, in particular no conditions arising from physical constraints. Clearly,
Link(A, B) and Link(B, A) are equivalent.
-
CountCritical() - return the number of critical rings for the current configuration of
linked rings.
출처:ioi/2012/day1
[질/답]
[제출 현황]
[푼 후(0)]



 Other configurations are clearly possible, since a ring can be linked to three or more other rings. We
say that a ring is critical if after opening and removing it, all remaining rings form a set of chains (or
there are no other rings left). In other words, there can be nothing but chains left.
Example
Consider the 7 rings in the next figure, numbered from 0 to 6. There are two critical rings. One
critical ring is 2: after its removal, the remaining rings form chains [1], [0, 5, 3, 4] and [6]. The other
critical ring is 3: after its removal, the remaining rings form chains [1, 2, 0, 5], [4] and [6]. If we
remove any other ring, we do not obtain a set of disjoint chains. For example, after removing ring
5: although we have that [6] is a chain, the linked rings 0, 1, 2, 3 and 4 do not form a chain.
Other configurations are clearly possible, since a ring can be linked to three or more other rings. We
say that a ring is critical if after opening and removing it, all remaining rings form a set of chains (or
there are no other rings left). In other words, there can be nothing but chains left.
Example
Consider the 7 rings in the next figure, numbered from 0 to 6. There are two critical rings. One
critical ring is 2: after its removal, the remaining rings form chains [1], [0, 5, 3, 4] and [6]. The other
critical ring is 3: after its removal, the remaining rings form chains [1, 2, 0, 5], [4] and [6]. If we
remove any other ring, we do not obtain a set of disjoint chains. For example, after removing ring
5: although we have that [6] is a chain, the linked rings 0, 1, 2, 3 and 4 do not form a chain.
