어느 시골에, 쌀의 길 이라고 불리는 긴 직선 도로가 있다. 이 길을 따라 R 개의 논들이 있다. 각 논들은 1 이상 L 이하의 정수좌표를 갖는다. 논들은 좌표 값이 감소하지 않는 순서로 주어진다. 즉, 0 ≤ i < R 에 대해서, 논 i 는 좌표 X[i] 에 있다. 1 ≤ X[0] ≤ ... ≤ X[R-1] ≤ L 라고 가정할 수 있다.
여러 개의 논이 하나의 같은 좌표에 있을 수 있음을 주의하라.
논에서 수확한 가능한 가장 많은 쌀들을 저장할 수 있는 하나의 쌀 창고를 세우려고 계획하고 있다. 논의 위치와 같이, 쌀 창고의 위치는 1 이상 L 이하의 정수좌표에만 있을 수 있다. 쌀 창고는 논들이 위치하고 있는 장소를 포함하여 어떤 곳에든지 세울 수 있다.
수확의 계절에 각 논들은 정확히 트럭 한대 분량의 쌀만 생산할 수 있다. 쌀들을 창고로 옮기기 위해서 트럭 운전사들을 고용하여야 한다. 트럭 운전사는 한 트럭분량의 쌀을 창고로 옮기는데 단위 거리당 1 바트의 요금을 청구한다. 다르게 말하자면, 논으로부터 쌀을 창고로 옮기는 비용은, 논의 좌표 값과 창고의 좌표 값의 차이와 같다. 불행히도, 올해의 예산이 충분하지 못하여 쌀의 수송에는 최대 B 바트 까지만 사용할 수 있다.
여러분이 해야 할 일은 가능한 가장 많은 쌀을 창고로 모으기 위한 창고의 위치를 결정하는 것이다.
쌀을 옮기는데 허용된 예산은 매우 클 수가 있음을 주의하라. 예산은 64-비트의 정수로 주어지고, 계산 과정에서는 64-비트의 정수를 사용하도록 권장한다. C/C++에서는 long long 데이터 형을 사용하고, 파스칼에서는 Int64 데이터 형을 사용하라.
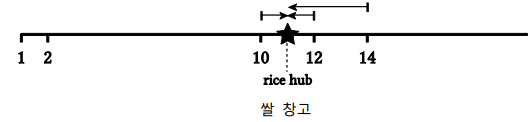
입력 5 20 6 1 2 10 12 14 출력 3

이 경우에는 창고의 위치에 대한 여러 개의 최적 위치가 있다: 10 이상 14 이하의 어느 정수 위치에든지 쌀 창고를 둘 수 있다. 위의 그림은 최적 위치들 중의 하나를 보여준다. 이 경우 10 과 12, 14 의 위치에 있는 논으로부터 쌀들을 옮길 수 있다. 어떤 최적의 창고 위치에 대해서든지, 쌀의 총 수송 비용은 6 바트 이하이다. 세 개보다 많은 논으로부터 쌀을 모을 수 있는 창고의 위치는 존재하지 않으므로, 이 답이 최적이고, 3 을 출력 해야 한다.
출처:ioi 2011 day1 3/3