프로그램 명: ioi_pyramid
제한시간: 5 초
//번역//
You have been asked to find the largest affordable location for constructing a new pyramid.? ?In order to
help you decide, you have been provided with a survey of the available land which has been conveniently
divided into an M by N grid of square cells. The base of the pyramid must be a square with sides parallel
to those of the grid.
The survey has identified a set of P possibly overlapping obstacles, which are described as rectangles in
the grid with sides parallel to those of the grid. In order to build the pyramid, all the cells covered by its
base must be cleared of any obstacles. Removing the i th obstacle has a cost Ci Whenever an obstacle is
removed, it must be removed completely, that is, you cannot remove only part of an obstacle. Also,
please note that removing an obstacle does not affect any other obstacles that overlap it.
TASK
Write a program that, given the dimensions M and N of the survey, the description of the P obstacles,
the cost of removing each of the obstacles, and the budget B you have, finds the maximum possible side
length of the base of the pyramid such that the total cost of removing obstacles does not exceed B.
CONSTRAINTS
Your program will be graded on three disjoint sets of tests. For all of them, the following constraints
apply:
-
1 <= M, N <= 1,000,000 The dimensions of the grid.
-
1 <= Ci <= 7,000 The cost of removing the i th obstacle.
-
1 <= Xi1 <= Xi2 <= M X coordinates of the leftmost and the rightmost cells of the i th obstacle.
-
1 <= Yi1 <= Yi2 <= N Y coordinates of the bottommost and the topmost cells of the i th obstacle.
입력
Your program must read from the standard input the following data:
- Line 1 contains two integers separated by a single space that represent M and N respectively.
- Line 2 contains the integer B, the maximum cost you can afford (i.e., your budget).
- Line 3 contains the integer P, the number of obstacles found in the survey.
- Each of the next P lines describes an obstacle. The i th of these lines describes the i th obstacle. Each
line consists of 5 integers: Xi1, Yi1, Xi2, Yi2, and Ci separated by single spaces. They represent
respectively the coordinates of the bottommost leftmost cell of the obstacle, the coordinates of
the topmost rightmost cell of the obstacle, and the cost of removing the obstacle.? ? The
bottommost leftmost cell on the grid has coordinates (1, 1) and the topmost rightmost cell has
coordinates (M, N).
출력
Your program must write to the standard output a single line containing one integer, the maximum
possible side length of the base of the pyramid that can be prepared. If it is not possible to build any
pyramid, your program should output the number 0.
입출력 예
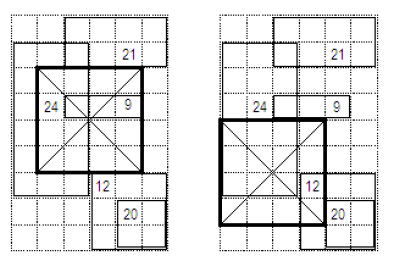
입력
6 9
42
5
4 1 6 3 12
3 6 5 6 9
1 3 3 8 24
3 8 6 9 21
5 1 6 2 20
출력
4
The figure shows two possible locations for the pyramid's base, both having a side of length 4.
 입력
13 5
0
8
8 4 10 4 1
4 3 4 4 1
10 2 12 2 2
8 2 8 4 3
2 4 6 4 5
10 3 10 4 8
12 3 12 4 13
2 2 4 2 21
출력
3
The figure shows the only possible location for the pyramid's base having a side of length 3.
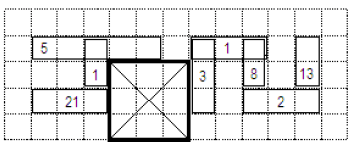
입력
13 5
0
8
8 4 10 4 1
4 3 4 4 1
10 2 12 2 2
8 2 8 4 3
2 4 6 4 5
10 3 10 4 8
12 3 12 4 13
2 2 4 2 21
출력
3
The figure shows the only possible location for the pyramid's base having a side of length 3.
출처: International Olympiad In Informatics 2008
[질/답]
[제출 현황]
[푼 후(0)]
 입력
13 5
0
8
8 4 10 4 1
4 3 4 4 1
10 2 12 2 2
8 2 8 4 3
2 4 6 4 5
10 3 10 4 8
12 3 12 4 13
2 2 4 2 21
출력
3
The figure shows the only possible location for the pyramid's base having a side of length 3.
입력
13 5
0
8
8 4 10 4 1
4 3 4 4 1
10 2 12 2 2
8 2 8 4 3
2 4 6 4 5
10 3 10 4 8
12 3 12 4 13
2 2 4 2 21
출력
3
The figure shows the only possible location for the pyramid's base having a side of length 3.

입력 13 5 0 8 8 4 10 4 1 4 3 4 4 1 10 2 12 2 2 8 2 8 4 3 2 4 6 4 5 10 3 10 4 8 12 3 12 4 13 2 2 4 2 21 출력 3 The figure shows the only possible location for the pyramid's base having a side of length 3.
