프로그램 명: ioi_gard
제한시간: 5 초

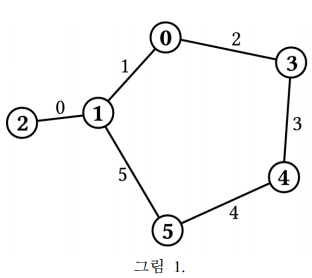
식물학자 철수는 여러 반의 학생들과 함께 태국 최대의 식물원을 방문하기로 하였다. 이 넓은 식물원은 (0 부터 N-1 까지의 번호가 붙은) N 개의 연못과 M 개의 산책로로 구성되어 있다.

각 산책로는 서로 다른 두 연못을 연결하며, 양방향으로 모두 이동하는 것이 가능하다. 어느 연못이든지 최소 하나의 산책로가 연결되어 있다. 이 산책로들에는 철수가 좋아하는 아름다운 식물들이 많이 있다. 같은 반의 학생들은 함께 이동하며, 각 반이 산책을 시작하는 연못은 서로 다를 수 있다.

철수는 아름다운 열대 식물들을 아주 좋아한다. 따라서, 철수와 각 반의 학생들은 어느 연못에서든 가장 아름다운 산책로를 선택하여 이용한다. 단, 그 산책로를 바로 직전에 이용할 경우에는 두번째로 아름다운 산책로를 이용한다.

하지만, 현재 연못에 연결된 산책로가 단 하나뿐인 경우는 두 번째로 아름다운 산책로가 존재하지 않으므로 방금 사용한 산책로를 다시 이용하는 것을 허용한다. 철수는 식물학자이므로 두 산책로의 아름다운 정도가 같은 경우는 없다.

학생들은 식물에는 큰 관심이 없다. 학생들의 관심은 어떤 연못 P 옆에 위치한 고급 식당에서 점심 식사를 하는 것이다.

철수는 각 반의 학생들이 정확히 K 개의 산책로를 지난 다음 배가 고파질 것이라는 것을 알고 있다. 각 반 마다 K 의 값은 다를 수 있다. 이 상황 하에서 철수는 각 반에 대해 정확히 K 개의 산책로를 이용 후 연못 P 에 도착하는 방법의 수가 얼마나 많은지 알고 싶다.

각 반에 대한 상황을 정리하면 다음과 같다

각 반이 P 로 가는 도중에 연못 P 를 지나는 것도 가능하다. 그러나, 마지막에는 반드시 P 에 도달하여야 한다.

제한 시간은 5 초이다.

입력

당신은 연못과 산책로에 대한 정보를 받아서 Q 개의 반에 대한 해답을 찾아야 한다. 즉, Q 개의 K 값에 대한 해답을 생성해야 하는 것이다.

출력

각 i(0 ≤ i < Q)에 대해서함수는 철수와 반 i 의 학생들이 정확히 G[i]개의 산책로를 이용한 후 연못 P 에 도달할 수 있는 모든 가능한 서로 다른 경로들의 갯수를 찾아야 한다.

각 반 i 에 대해서 함수는 반 i 의 경로의 수가 X 라는 의미로 X 를 출력해야 한다. 출력 순서는 배열 G 에 주어진 순서와 동일해야 한다. 어떤 반에 대해 가능한 경로가 없는 경우는 0 을 출력해야 한다

입출력 예

입력

6 6 0
1 2
0 1
0 3
3 4
4 5
1 5
1
3

출력

2

입력

5 5 2
1 0
1 2
3 2
1 3
4 2
2
3 1

출력

1 2

입출력 보충

입출력 예 1.

산책로의 번호가 작을 수록 더 아름답다는 것에 주의하자. 즉, 산책로 0 이 가장 아름다운 것이고, 산책로 1 이 그 다음으로 아름다운 것임을 알수 있다.

산책로의 개수가 3 이고 연못 0 에서 끝나면서 이동 규칙을 만족하는 경로는 다음의 두가지 경우 밖에 없다.

첫번째 경로는 연못 1 에서 시작한다. 그 곳에서 가장 아름다운 산책로를 택하면 연못 2 로 가게 된다. 연못 2 에서는 연못 1 로 가는 방법 밖에는 없다. 이제 연못 1 에서는 방금 사용한 산책로를 제외하면 연못 0 으로 가는 산책로를 택하게 되어 목적지에 도착할 수 있다. 이 경우에 2 를 출력하여야 한다.

입출력 예2.

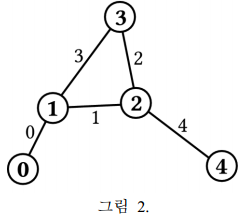
첫번째 반에 대해서 3 개의 산책로를 이용하여 연못 2 에 도착하는 방법은 하나 밖에 없으며 다음과 같다: 1 → 0 → 1 → 2.

두번째 반에 대해서 1 개의 산책로를 이용하여 연못 2 에 도착하는 방법은 다음의 두가지가 있다: 3 → 2 와 4 → 2. 따라서, 정확한 프로그램은 첫 번째 반에 대해 1을 출력하고 두 번째 반에 대해 2 를 출력해야 하며 정확한 출력 순서를 지켜야 한다. 

출처:ioi 2011 day1 1/3
[질/답] [제출 현황] [푼 후(3)]
[ 채 점 ] [홈으로]  [뒤 로]