두 사람 바자(Bazza)와 샤자(Shazza)가 다음 게임을 하고 있다. 각 셀에는 음이 아닌 정수가 쓰여 있고, 게임이 시작될 때 모든 셀의 값은 0이다.

이 게임은 다음과 같이 진행된다. 게임 진행 중에, 바자는 다음 두 가지 중 하나를 할 수 있다.

• 셀 (P, Q) 의 값을 업데이트한다. 즉, 이 셀에 쓰여진 정수를 바꾼다.
• 샤자에게 주어진 직사각형 모양의 셀들 안의 모든 정수들의 (직사각형의 마주보는 양 모퉁이 (P, Q) , (U, V) 를 포함) 최대공약수(GCD)를 계산하도록 요청한다.

당신의 임무는 정답을 구하는 것이다.

예시

• 셀 (0, 0) 을 20으로 업데이트
• 셀 (0, 2) 를 15로 업데이트
• 셀 (1, 1) 을 12로 업데이트

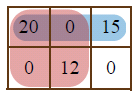
이 결과는 위 그림과 같다. 그리고 바자는 다음 직사각형에 대해 최대공약수가 무엇인지 질의한다.

• 양 모퉁이 (0, 0) , (0, 2) : 이 직사각형 안의 세 정수는 20, 0, 15이고 최대공약수는 5이다.
• 양 모퉁이 (0, 0) , (1, 1) : 이 직사각형 안의 네 정수는 20, 0, 0, 12이고 최대공약수는 4이다.

• 셀 (0, 1) 을 6으로 업데이트
• 셀 (1, 1) 을 14로 업데이트

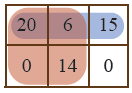
• 양 모퉁이 (0, 0) , (0, 2) : 이 직사각형 안의 세 정수는 이제 20, 6, 15이고 최대공약수는 1이다.
• 양 모퉁이 (0, 0) , (1, 1) : 이 직사각형 안의 네 정수는 20, 6, 0, 14이고 최대공약수는 2이다.

입력

• 첫 줄에는 행의 크기 R , 열의 크기 C , 질의와 업데이트의 수 N 이 주어진다. 1 ≤ R, C ≤ 10^9 , 0 ≤ K ≤ 10^18 . 여기서 K 는 바자가 그리드 셀에 써넣는 숫자이다.
• 다음 N 줄의 첫 수는 1 혹은 2 이고 1 은 업데이트 , 2 는 질의를 의미 한다. 1 이 주어지는 줄에는 세 개의 수(셀의 정보와 업데이트 수)가 , 2 가 주어지는 줄에는 4 개의 수(시작셀 , 끝셀)가 주어진다.

출력

입출력 예

입력

2 3 9
1 0 0 20
1 0 2 15
1 1 1 12
2 0 0 0 2
2 0 0 1 1
1 0 1 6
1 1 1 14
2 0 0 0 2
2 0 0 1 1

출력

5
4
1
2

출처:ioi 2013