이 이야기는 세상의 태초에, IOI라는 것은 꿈꿀 수도 없었던 아주 먼 옛날에 생긴 일이다.
0, …, N - 1 까지 번호가 붙여진 N 개의 빌라봉(호수)이 있는 땅에 큰 뱀이 살고 있다. 이 땅에는 M 개의 길이 있고, 각각의 길은 한 쌍의 빌라봉을 연결하며, 이 길 을 통해 뱀은 양방향으로 이동할 수 있다. 임의의 빌라봉 쌍은 길을 따라서 (직접 또는 간접적으로) 최대 하나의 경로로 연결이 되어 있다. 단, 어떤 빌라봉 쌍들은 연결되어 있지 않을 수도 있다 (즉, M ≤ N - 1 이다). 뱀이 하나의 길을 지나가는 데 에는 몇 일의 시간이 걸리는데, 이 시간은 길마다 다를 수 있다.
뱀의 친구 캥거루는 N - M - 1 개의 새로운 길을 만들어 뱀이 모든 빌라봉 쌍 사이를 오갈 수 있도록 하고 싶다. 캥거루는 임의의 두 빌라봉을 선택하여 그 사이에 길을 만들 수 있으며, 캥거루가 만든 길을 통행하는 데에는 항상 L 일이 걸린다. 캥거루는 또한 뱀이 최대한 빨리 이동할 수 있기를 원한다. 캥거루는 임의의 두 빌 라봉 사이를 오가는데 드는 최대 시간이 최소가 되도록 길을 만들 것이다. 캥거루 가 이렇게 길을 만든 뒤 뱀이 두 빌라봉 사이를 오가는데 드는 최대 시간을 계산하시오.
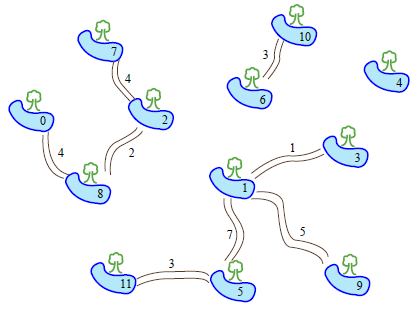
예를 들면

위 그림에는 N = 12 개의 빌라봉과 M = 8 개의 길이 있다. 새로 만들어지는 길을 뱀이 통행하는 데에는 2일이 걸린다고 가정하자 (즉, L = 2 이다).
그러면 캥거루는 아래와 같이 세 개의 길을 만들 수 있다.
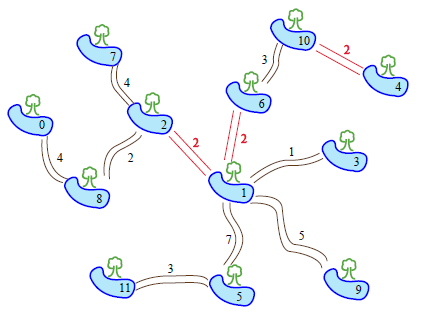
모든 길이 만들어진 뒤의 모습이 위 그림에 나타나 있다. 여기서 두 빌라봉 사이의 최대 통행 시간은 18일인데 (빌라봉 0과 11 사이), 이것이 가능한 가장 작은 값이다. 즉, 캥거루가 어떤 식으로 새로운 길을 만들더라도, 뱀이 통행하는 데 18일 이 상이 걸리는 빌라봉 쌍이 항상 존재한다.
입력 12 8 2 0 8 4 8 2 2 2 7 4 5 11 3 5 1 7 1 3 1 1 9 5 10 6 3 출력 18
출처: ioi 2013