프로그램 명: ioi_city
제한시간: 1 초

당대의 많은 이탈리아 과학자들과 예술가들처럼 다빈치는 도시 계획과 디자인에 대단한 관심이 있었다. 다빈치는 편안하고, 공간을 넓고 합리적으로 사용하며, 중세 시대 도시의 좁고 답답함과는 거리가 먼 이상적인 도시를 디자인할 계획을 가지고 있었다

이상적인 도시

무한 개 네모 셀들의 격자 위에 N 개의 블럭들을 놓아서 도시를 만든다. 각 셀은 좌표들의 쌍 (행, 열)로 나타낸다. (i, j) 셀이 주어지면, 인접한 셀들은 (i-1, j), (i+1, j), (i, j-1) 그리고 (i, j+1) 이다. 그리드 위에 놓여질 때, 각 블럭은 정확히 하나의 셀을 덮는다. 블럭은 1 ≤ i, j ≤ 2^31 - 2 인 셀 (i, j) 에만 놓을 수 있다. 셀들 위에 놓여진 블럭들을 나타낼 때, 셀들의 좌표를 사용할 것이다. 두 블럭이 서로 인접한 셀들에 놓여지면 두 블럭은 인접했다고 말한다. 이상적인 도시에서 모든 블럭들은 도시안에 구멍이 없도록 연결된다. 다시 말해서, 셀들은 아래의 조건들을 만족해야만 한다. 임의의 두 비어있지 않은 셀들에 대해서, 인접한 비어있지 않은 셀들로만 이동하는 방법으로 한 셀에서 다른 셀에 도달할 수 있는 경로가 적어도 하나 이상 존재한다.

예제 1

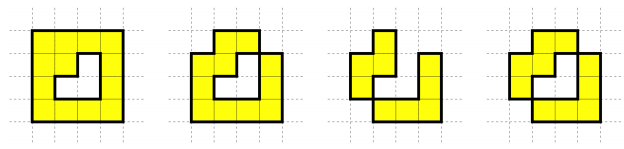
아래 그림 모두는 이상적인 도시가 아니다. 처음 두 개는 첫번째 조건을 만족하지 않고, 세 번째 그림은 두번째 조건을 만족하지 않고, 네번째 그림은 두 조건 모두를 만족하지 않는 다.

거리

도시 안을 이동할 때, 걸음은 한 블럭에서 인접한 블럭으로 이동하는 것을 말한다. 비어있는 셀들로는 이동할 수 없다. v , v , …, v 을 그리드 위에 놓여 있는 N 개 블럭들의 좌표 라고 하자. 좌표 v 와 v 를 가진 임의의 서로 다른 두 블럭들에 대해서, 그들간의 거리 d(v , v )는 이 블럭들 중 하나에서 다른 곳으로 가는데 요구되는 걸음들의 최소 수로 정의된다.

예제 2

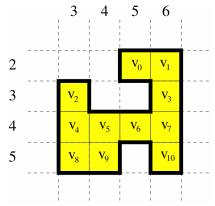
아래 그림은 좌표 v = (2, 5), v = (2, 6), v = (3, 3), v = (3, 6), v = (4, 3), v = (4, 4), v = (4, 5), v = (4, 6), v = (5, 3), v = (5, 4), 그리고 v = (5, 6) 를 가지는 N = 11 개의 블럭들로 이루어 진 이상적인 도시를 나타낸다. 그러면, d(v , v ) = 1, d(v , v ) = 6, d(v , v ) = 2, 그리고 d(v , v ) = 4 이다.

해야 할 일

당신은 주어진 이상적인 도시에 대하여 모든 가능한 i < j 인 두 블럭 쌍 v 와 v 에 대한 거리들의 합을 계산하는 프로그램을 작성해야 한다. 정확히 말하면, 프로그램은 다음의 합을 계산해야 한다.
Σ d(v , v ), 단, 0 ≤ i < j ≤ N - 1
구체적으로, 도시를 나타내는 N 과 두 배열 X 와 Y 가 주어 질때, 위 공식을 계산하는 함수 DistanceSum(N, X, Y) 를 구현해야 한다. 배열 X 와 Y 는 크기 N 이고, 0 ≤ i ≤ N - 1 에 대해서, 블럭 i 는 좌표 (X[i], Y[i])를 가지고 1 ≤ X[i], Y[i] ≤ 2^31 - 2 이다. 결과가 32비트를 사용 해서 표현하기에 너무 클 수 있기 때문에 결과를 1,000,000,000 으로 나눈 나머지로 계산한다.

예제 2에서 11 × 10 / 2 = 55 개의 블럭 쌍이 존재한다. 모든 쌍 간의 거리들의 합은 174 이다.

grader 예시

주어지는 grader의 입력 양식은 다음과 같다.

입출력 예

입력

11
2 5
2 6
3 3
3 6
4 3
4 4
4 5
4 6
5 3
5 4
5 6

출력

174
Leonardo, like many other Italian scientists and artists of his age, was extremely interested in city planning and urban design. He aimed to model an ideal city: comfortable, spacious and rational in its usage of resources, far away from the narrow, claustrophobic cities of the Middle Ages.

The ideal city

The city is made of N blocks placed on an infinite grid of cells. Each cell is identified by a pair of coordinates (row, column). Given a cell (i, j), the adjacent cells are: (i - 1, j), (i + 1, j), (i, j - 1), and (i, j + 1). Each block, when placed onto the grid, covers exactly one of the cells. A block can be placed onto the cell (i, j) if and only if 1 ≤ i, j ≤ 2^31 - 2. We will use the coordinates of the cells to also refer to the blocks on top of them. Two blocks are adjacent if they are placed in adjacent cells. In an ideal city, all of its blocks are connected in such a way that there are no “holes” inside its border, that is, the cells must satisfy both conditions below. For any two empty cells, there exists at least one sequence of adjacent empty cells connecting them. For any two non-empty cells, there exists at least one sequence of adjacent non-empty cells connecting them.

Example 1

None of the configurations of blocks below represent an ideal city: the first two on the left do not satisfy the first condition, the third one does not satisfy the second condition, and the fourth one does not satisfy either of the conditions.

Distance

When traversing the city, a hop indicates going from one block to an adjacent one. Empty cells cannot be traversed. Let v?, v₁, …, v be the coordinates of the N blocks placed on the grid. For any two distinct blocks at coordinates v and v , their distance d(v , v ) is the smallest number of hops that are required to go from one of these blocks to the other one. N - 1 i j i j

Example 2

The configuration below represents an ideal city made of N = 11 blocks at coordinates v = (2, 5), v = (2, 6), v = (3, 3), v = (3, 6), v = (4, 3), v = (4, 4), v = (4, 5), v = (4, 6), v = (5, 3), v = (5, 4), and v = (5, 6). For example, d(v , v ) = 1, d(v , v ) = 6, d(v , v ) = 2, and d(v , v ) = 4.

Statement

Your task is to, given an ideal city, write a program to compute the sum of all pairwise distances between blocks v and v for which i < j. Formally, your program should compute the value of the following sum:
∑ d(vi, vj), where 0 ≤ i < j ≤ N - 1
Specifically, you have to implement a routine DistanceSum(N, X, Y) that, given N and two arrays X and Y that describe the city, calculates the formula above. Both X and Y are of size N; block i is at coordinates (X[i], Y[i]) for 0 ≤ i ≤ N - 1, and 1 ≤ X[i], Y[i] ≤ 2^31 - 2. Since the result may be too big to be represented using 32 bits, you should report it modulo 1 000 000 000 (one billion).

In Example 2, there are 11 × 10 / 2 = 55 pairs of blocks. The sum of all the pairwise distances is 174. 

출처:ioi/2012/day2/1번 문제
[질/답] [제출 현황] [푼 후(0)]
[ 채 점 ] [홈으로]  [뒤 로]