1부터 N 까지 번호가 붙여진 N 개의 마을과 이들 마을을 연결하는 도로망이 있다. 이 도로망에서는, 각 마을로부터 다른 모든 마을까지 가는 경로는 하나뿐이다. 각 마을에 사는 사람들의 수와 각 도로를 지나는데 걸리는 시간이 주어진다. 그리고 이들 마을 중 서로 다른 두 마을에만 병원이 있다.

마을 A에서 마을 B까지 가는데 걸리는 시간은 A에서 B까지의 경로 상에 있는 도로들의 통행시간의 합이다.

예를 들어, 다음과 같은 도로망을 고려해 보자.

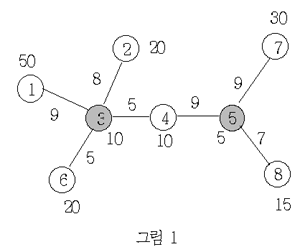
동그라미는 마을을 나타내고, 동그라미 안에 있는 수는 마을의 번호이고, 바깥에 있는 수는 마을에 있는 사람들의 수이다. 선분은 도로를 나타내고, 선분 상의 수는 도로의 통행시간을 나타낸다. 또한 병원이 세워져 있는 두 마을은 회색으로 칠해져 있다.

예산을 도로개선에 투입하여 도로의 통행시간을 줄일 수 있다. 이때 각 도로는 예산 C 를 들이면 통행시간을 C 시간 만큼 줄일 수 있다. 이제 다음의 제약조건을 만족하면서 전체 예산 B 를 도로개선에 투입한다.

제약조건:

1. 도로에 예산을 아무리 많이 사용하더라도 각 도로의 통행시간을 L 미만으로 할 수는 없다.
2. 도로개선에 사용하는 전체예산은 B 이하이어야 한다.

이 때, 위의 제약조건을 만족하면서 다음 두 질문의 답을 구하는 프로그램을 작성하시오.

• 질문 1: 각 사람이 가까운 병원까지 가는데 걸리는 시간의 합이 가장 작도록 할 때, 시간의 합의 최소값은 얼마인가?
• 질문 2: 각 사람이 가까운 병원까지 가는데 걸리는 시간 중 가장 긴 시간이 최소가 되도록 할 때, 그 최소 시간은 얼마인가?

• 질문 1의 해는 도로 (1,3)에 예산 3을 사용하여 도로 (1,3)의 통행시간을 6으로 만들고, 도로 (2,3)에 예산 1을 사용하여 통행시간을 7로 만들고, 예산 3을 도로 (5,7)에 사용하여 통행시간을 6으로 만들면 각 사람이 병원을 이용하는데 걸리는 시간의 합은 50*6 + 20*7 + 10*5 + 20*5 +30*6 + 15*7 = 875이다.
• 질문 2의 해는 도로 (1,3), (4,5), (5,7)에 각각 비용 2를 사용하고, 도로 (2,3)에 비용 1을 사용하면 각 사람이 가까운 병원까지 가는데 걸리는 가장 긴 시간은 7이 된다. 어떻게 하더라도 위의 두 답보다 좋게 할 수 없다.

프로그램의 실행시간은 1초를 넘을 수 없다. 한 질문의 답만 맞을 경우 부분 점수가 주어진다.

입력

• 첫 번째 줄에 B (1≤ B ≤4,000,000)와 L (1≤ L ≤1,000)을 나타내는 두개의 양의 정수가 빈칸을 사이에 두고 주어진다.
• 두 번째 줄에 마을의 수 N (2≤ N ≤4,000)이 주어진다.
• 세 번째 줄에 마을 1부터 마을 N 까지 각 마을에 사는 사람들의 수(1 이상 500 이하)가 빈칸을 사이에 두고 차례로 주어진다.
• 그 다음 줄부터 N-1 개의 각 줄에 도로의 정보 즉, 도로의 양끝 마을 번호와 도로의 통행시간(1 이상 1,000 이하)을 나타내는 세 개의 양의 정수가 빈칸을 사이에 두고 차례로 주어진다. 마지막 줄에 병원이 있는 서로 다른 두 마을의 번호가 빈칸을 사이에 두고 주어진다.

출력

입출력 예

입력

7 6
8
50 20 10 10 5 20 30 15
1 3 9
3 2 8
3 4 5
4 5 9
7 5 9
8 5 7
3 6 5
3 5

출력 

875
7

출처: 제27회한국정보올림피아드시?도지역본선(2010.5.29) 중등부문제5