프로그램 명: fourier_line
제한시간: 1 초

조셉 푸리에는 위대한 수학자이자 물리학자 였다. 그는 푸리에 급수로 널리 알려져 있다.

그는 19 명의 아이들 중에 가장 어렸고 총명 했으며 어렸을때부터 수학에 많은 관심을 보이기 시작했다. 성장 한 후에는 Auxerre 에 수학교수인 C.Bonard 와 편지를 주고 받았다.

한 편지에서 푸리에는 다음과 같은 질문을 했다.

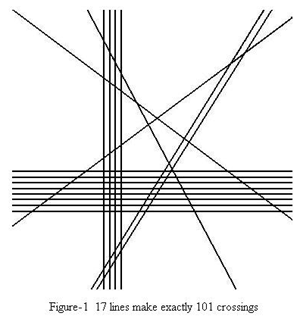
평면에서 17 개의 라인을 그어서 정확히 101 개의 교점을 어떻게 만들수 있는가? 각 교점은 정확이 두 개의 직선으로 만들어 진다.
물론 이것은 쉬운 문제이다. 아래 그림은 그의 요구를 만족하는 그림이다.

우리가 풀어야 할 문제는 N 개의 직선을 그어 정확히 M 개의 교점을 만들어 내는가이다. 각 교점은 두 개의 직선만이 공유한다. 그리고 가능한 경우 이 직선들이 평면을 많아야 몇개를 만들수 있는가 를 알아내는 것이다.

입력

The input may have several sets of test data.

각 테스트데이터에는 두 개의 수 N,M(1 <= N <= 100, 0 <= M <= 10000) 이 주어진다. 테스트 데이터의 마지막에는 0 0 이 주어진다.

출력

다음과 같은 형식으로 출력한다. N,M 의 개수가 하나인 경우에도 "lines" , "crossings" 로 출력한다.(복수)

입출력 예

입력

4 3
4 6
4 2
5 11
17 101
0 0

출력

Case 1: 4 lines with exactly 3 crossings can cut the plane into 8 pieces at most.
Case 2: 4 lines with exactly 6 crossings can cut the plane into 11 pieces at most.
Case 3: 4 lines cannot make exactly 2 crossings.
Case 4: 5 lines cannot make exactly 11 crossings.
Case 5: 17 lines with exactly 101 crossings can cut the plane into 119 pieces at most. 

출처:Beijing 2004 Preliminary@POJ
채점데이터:august14
[질/답] [제출 현황] [푼 후(0)]
[ 채 점 ] [홈으로]  [뒤 로]