[문제 요약] n=4 인 경우 그림과 같은 구조로 타일이 주어질 때 1 번 타일에서 마지막 타일까지 가는 최단 길의 패스를 구하는게 문제이다.

각 타일은 앞, 뒤로 두개의 수가 주어지고 수가 같은 경우 인접한 타일로 이동이 가능하다. 1 번 타일에서 시작해야 하고 마지막 타일까지 가지 못하는 경우 가능한 최대 번호를 가지는 타일로 가야 하고 여러개의 길이 존재하는 경우 그 중 하나를 출력한다.

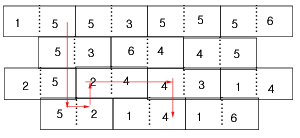
The Totem is situated on the opposite side of the hall form the entrance. The floor of the hall is covered with stone tiles that bear a striking resemblance to domino tiles. Each tile is divided into two halves (squares), and each half has a number from one to six, inclusive, chiseled into it. Tiles are arranged in N rows, with N tiles in each odd-numbered row and N - 1 tiles in each even-numbered row. The image below corresponds to the first test example (N = 5):

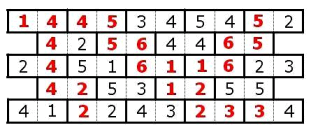
It is only possible to step from one tile to an adjacent one if the two tiles have matching numbers on halves that share an edge. Help Mister No find the shortest path to the Totem by determining the sequence of tiles (outputting the sequence of tiles' labels, described below) that need to be stepped on, in order, from the first to the last tile on the path.

If there is no possible path to the Totem, find the shortest path to the tile with the largest label (so that Mister No can make a heroic jump). The stone tiles are labelled in row-major order: in the first row, the first tile has the label 1, and the last one N; in the second row, the first tile is N + 1, and the last one 2*N - 1, and so on. The entrance leads to the tile with label 1, and the totem is on the last tile in the last row. Mister No always starts from the entrance.

입력

• The first line of input contains the positive integer N (1 ≤ N ≤ 500), the number of stone tile rows.
• Each of the following N * N - N / 2 lines (where “/” stands for integer division) contains two positive integers Ai and Bi (1 ≤ Ai , Bi ≤ 6, 1 ≤ i ≤ N * N - N / 2), the values chiseled into the left and right halves, respectively, of tile i.

출력

• The first line of output must contain the length (in tiles) of the required shortest path.
• The second line of output must contain a sequence of space-separated positive integers, the labels of tiles on the shortest path. As there can exist more than one shortest path, output any one of them.

입출력 예

input

5
1 4
4 5
3 4
5 4
5 2
4 2
5 6
4 4
6 5
2 4
5 1
6 1
1 6
2 3
4 2
5 3
1 2
5 5
4 1
2 2
4 3
2 3
3 4

output

7
1 2 7 12 17 22 23

input

3
1 2
2 3
6 6
2 4
3 5
6 6
4 5
5 6

output

4
1 2 5 8

input

4
1 5
5 3
5 5
5 6
5 3
6 4
4 5
2 5
2 4
4 3
2 4
5 2
1 4
1 6

output

7
1 5 8 12 9 10 13

출처:coci/2012-2013/contest5 3번/6
special judge:functionx