프로그램 명: coci_mnogomet(special judge)
제한시간: 1 초 

[요약 중]

2N 명의 사람이 두 팀으로 나뉘어 축구를 하고 있다.


각 선수는 팀 명이 붙은 유니폼과 1 .. N 의 등번호가 붙은 옷을 입고 있다.

각 선수마다 그의 정확도를 안다. 그가 볼을 패스할 수 있는 팀메이트 F와 그에게수 공을 뺏을 수 있는 적들의 집합 E  ..


선수가 볼을 소유할 때 정확히 일 초 후 다음 일들이 일어난다.



o 선수는 집합 F 에서 있는 선수들 중 한 명에게 볼을 패스 한다.

o E 에 속한 적군의 한 사람이 그의 볼을 뺏아간다.


o 선수가 슛을 시도한다.



슛을 시도할 때 골인이 될 확률은 그의 정확도와 같다.


슛 후, 골인이든 아니든 볼은 상대팀 1 번선수에게 넘어간다.




    다른 이벤트의 확률은 |F| : |E| : 1 순으로 비례한다.
    
    
    and depend only on the player currently in possession of the ball

    
    (|S| determines the size of the set S corresponding to the current player),

|S| 는 현재 선수에  대응하는 선수 집합 S 의 크기를 결정한다.
    
    
    

    not on any previous events in the game.

    게임에서 전의 이벤트가 아니고 
    
    
    The word  “random” means 

    단어 "random" 은 의미한다.
    
    that all players from the set F (or E) have the  same probability of being passed (or taking) the ball by (from) the player that is currently in the ball's possession.
    
    
    The time that a ball spends outside of a  player's possession is negligible.

    선수의 소유 밖인 시간은 무시할수 있다.





시합은 첫 번째 팀의 1 번 선수부터 시작하고 한 팀이 R 골을 넣거나 T 초가 경과하면 끝난다.


For  each possible final score, determine the probability that the match will end with it.

가 가능한 마지막 스코어에서 확률을 결정하라 시합이 그것과 같이 끝난다...



다음 그림은 선수들의 어레인지먼트를 나타낸다. 두 번의 테스트 샘플:
입력은 첫 번째 입력 예시이다. 
1 1 2
0.5 0 1 1
0.5 0 1 1

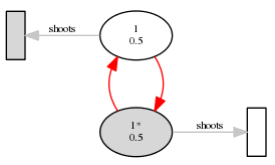
스타는 겜 시작시 볼을 소유하고 있는 선수를 가리킨다. 시합은 T = 2 초 동안 지속되고 혹은 어떤 사람이 R = 1 골을 넣는다면 . N= 1 이기 때문에 시합은 두 사람만이 한다. 양 쪽 선수는 0.5 의 확률을 가진다. 이것은 의미한다. 각각은 슛을 할 때 50 % 확률을 가진다. 그 이후에 볼은 상대방으로 넘어간다. 회색 플레이어를 흰색을 B 로 레이벌한다. 이 가정하에 , 단지 6 번의 가능한 매치가 가능하다. 각각에 대응하는 확률이다.
0.25 A decides to shoot and scores! 1:0
0.25 * 0.25 A decides to shoot, but misses.
B decides to shoot and scores! 		0:1
0.25 * 0.25 A decides to shoot, but misses.
B decides to shoot, but also misses. 		0:0
0.50 * 0.25 A loses the ball to B.
B decides to shoot and scores! 		0:1
0.50 * 0.50 A loses the ball to B.
B loses the ball to A. 		0:0
0.50 * 0.25 A loses the ball to B.
B decides to shoot, but misses. 		0:0

By summing probabilities for particular final results, we obtain the following solution:

0:0 0.25 * 0.25 + 0.5 * 0.5 + 0.5 * 0.25 0.5625
0:1 0.25 * 0.25 + 0.5 * 0.25 0.1875
1:0 0.25 0.25

정답과의 허용오차는 0.000001 이다.

2N people are playing football (soccer), divided into two teams. Each player wears a dress with the team logo and a unique (in the team) positive integer between 1 and N, inclusive. For each player, we know his precision, the set of teammates whom he can pass the ball to (F) and the set of opponents who can take the ball from him (E). When a player comes into possession of the ball, after exactly one second one of the following events will happen: 
o the player passes the ball to a random teammate from the set F,
o a random opponent from the set E takes the ball from him,
o the player attempts a shot at the goal.
If the player attempts a shot, the probability of scoring a goal is equal to his precision. After the shot, whether it was successful or not, the ball is awarded to the player number 1 from the opposing team.

The probabilities of different events are in the proportion |F| : |E| : 1, in order, and depend only on the player currently in possession of the ball (|S| determines the size of the set S corresponding to the current player), not on any previous events in the game. The word “random” means that all players from the set F (or E) have the same probability of being passed (or taking) the ball by (from) the player that is currently in the ball's possession. The time that a ball spends outside of a player's possession is negligible.

The match begins with player 1 from the first team in possession of the ball and ends either when one team has scored R goals or when T seconds have elapsed, whichever happens first. For each possible final score, determine the probability that the match will end with it. The following image illustrates the player arrangement for the second test example:

입력

출력

The match can theoretically end with one of R * (R + 2) different final results.

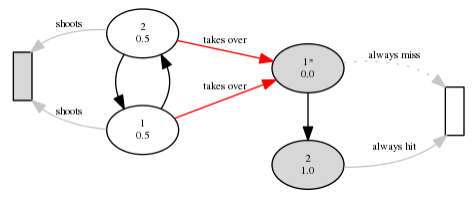
For each result, output the probability of its realization as a real number, one per line. Order the results first by the number of goals scored by the first team, then by the number of goas scored by the second team, in ascending order.

The permitted difference from the exact value for each probability is 0.000001.

입출력 예

input

1 1 2
0.5 0 1 1
0.5 0 1 1

output

0.56250
0.18750
0.25000

input

2 2 5
0.0 1 2 2 1 2
1.0 0 0
0.5 1 0 2
0.5 1 0 1

output

0.2578125
0.2812500
0.0703125
0.1718750
0.1640625
0.0234375
0.0156250
0.0156250

Clarification of the first example: 


The star denotes the player in possession of the ball in the beginning. The match lasts for only T = 2 
moves or until someone scores R = 1 goal. Since N = 1, there are only two players in the match, 
playing one against the other. Both players have the precision of 0.5, which means that each has a 50% 
chance of scoring a goal when trying to shoot, after which the ball is awarded to the opponent.
Let us label the grey player as A, and the white player as B. Under these assumptions, there are only 6 
possible matches. Each of them is described in the table below, with the corresponding probability, 
description and outcome:





 0.25  A decides to shoot and scores!  1:0 





 0.25 * 0.25  A decides to shoot, but misses.

B decides to shoot and scores!
0:1





 0.25 * 0.25 A decides to shoot, but misses.

B decides to shoot, but also misses.
0:0





0.50 * 0.25 A loses the ball to B. 

B decides to shoot and scores!

 0:1 





 0.50 * 0.50 A loses the ball to B.

B loses the ball to A.

 0:0





 0.50 * 0.25 A loses the ball to B.

B decides to shoot, but misses.

 0:0 





By summing probabilities for particular final results, we obtain the following solution:





0:0  0.25 * 0.25 + 0.5 * 0.5 + 0.5 * 0.25 0.5625





0:1 0.25 * 0.25 + 0.5 * 0.25 0.1875





1:0 0.25 0.25





출처:coci/2012-2013/contest5 6번/6
[질/답] [제출 현황] [푼 후(0)]
[ 채 점 ] [홈으로]  [뒤 로]