[요약] 미르코와 슬라브코는 자기들이 각각 가지고 있는 탑들을 같은 모양으로 만드려고 합니다. 그 모양은 양 끝에 있는 탑이 가장 높고 안으로 들어갈수록 하나씩 줄어드는 모양입니다. 둘은 탑들의 가장 위에 있는 블럭들 중 하나를 없애거나 상자에서 블럭을 가져와 원하는 탑의 가장 위에 놓을 수 있습니다.

최소 몇 번 블럭을 놓거나 없애야 조건에 맞는 같은 높이의 두 탑을 쌓을 수 있는지 출력하세요.

입력

• 첫 번째 줄에 탑의 길이 N (1 ≤ N ≤ 300 000)이 주어집니다.
• 두 번째 줄에 미르코의 탑 높이 정보가 순서대로 주어집니다. (0 ≤ mi ≤ 10^12)
• 세 번째 줄에 슬라브코의 탑 높이 정보가 순서대로 주어집니다. (0 ≤ si ≤ 10^12)

미르코가 첫번째 탑에 2개를 놓고 슬라브코가 세 번째 탑에 1개를 놓으면 높이 3 2 3 모양의 탑이 만들어집니다.

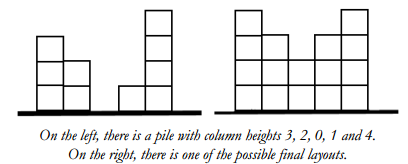
They have decided to create two equal piles constructed in a way that the heights of columns are strictly descending at first and then strictly ascending (see right image below) and the heights of adjacent columns differ exactly by 1 (see image). The lowest of the columns must have an equal number of columns to the left and to the right of it.

The piles can be modified by removing one brick from the top of some column and throw it out the window (they cannot reuse it) or by taking one brick from the box and place it on the top of some column (there is an infinite amount of bricks in the box). Removing or placing a brick counts as one move.

You have to determine the minimal number of moves so that Mirko and Slavko can rearrange their piles in the described way

input

• The first line of input contains an odd number N. (1 ≤ N ≤ 300 000), the number of columns in both piles.
• The second line of input contains N integers mi (0 ≤ mi ≤ 10^12), column heights in Mirko's pile.
• The third line of input contains N integers si (0 ≤ si ≤ 10^12), column heights in Slavko's pile.

OUTPUT

SAMPLE TESTS

input 
 
3 
1 2 3 
3 2 2 
 
output 
 
3 
input 
 
5 
2 3 0 1 4 
3 3 2 3 1 
 
output 
 
10 

Clarification of the first example: Mirko places two bricks on the top the first column in his pile and 
Slavko places one brick on the top of the third column in his pile.

출처:coci/2013-2014/contest6 3번
요약:ladown21