프로그램 명: coci_holmes(special judge)
제한시간: 1 초
[문제 요약]
1 번 입출력 예
3 2 1
1 2
2 3
2
3 건의 사건 발생. 2 건의 인과 관계 . 발생한 사건의 수
2 건의 인관 관계
1 3
2 3
발생한 사건 번호
2
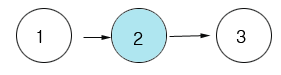
2 번 사건이 발생 했으므로 1 2 3 번 사건이 발생 했다고 유추 가능함.
2 번 입출력 예
3 2 1
1 3
2 3
3
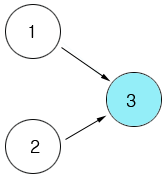
3 번 사건이 발행 했을 때 1 , 2 번 사건 중 어느 사건이 발생한지를 확정적으로 말할 수는 없다. 그래서 답은 3
단 , 입력의 인과 관계는 사이클이 발생하지 않는다.
Sherlock Holmes is a renowned detective. His Scotland Yard colleagues often
provide him with a set of evidence and ask for his help in solving the
mysteries. After many years of practice, Holmes has gained an enormous
amount of experience and already knows causes for many common events,
which, combined with his extraordinary deductive capabilities, enables him to
solve cases in a matter of minutes, from the comfort of his chair.
Holmes' knowledge base can be modeled as a set of implications of the form A->B
(where A and B represent events), which means that, if A occurred,
event B must have also occurred (remember that logical implication is false
only if A is true and B is false). Of course, implications can form chains of
reasoning, e.g. A->B->C . However, there will never be a circular chain of
implications (e.g. A->B->C->...->A ).
Holmes is given a set S = {S1, S2, S3, ..., Sn} of events that are known
to have occurred. He can then, using his extensive knowledge and deductive
powers, find all events that have certainly occurred.
It's important to note that Holmes' knowledge is so mind-bogglingly huge
that he knows all possible causes of events. In other words, there is no
implication that is true, but not included in Holmes' knowledge base.
Many detective agencies would highly appreciate Holmes' one of a kind
capabilities, so you were given a task to accomplish with a computer what is
out of reach for ordinary mortals. Write a program to find all events that have
certainly occurred based on the given implications and evidence collected by
your colleague detectives.
입력
-
First line of input consists of three integers, D (1 ≤ D ≤ 1000), the number of
different types of events, M (1 ≤ M ≤ 100000), the number of implications,
and N (1 ≤ N ≤ D), the number of evidence collected by the detectives.
-
Each of the M lines that follow contains two integers A and B (1 ≤ A, B ≤ D),
describing an implication A->B.
-
Finally, each of the last N lines contain an integer X (1 ≤ X ≤ D) describing
an event that must have occurred, based on the evidence collected by
detectives.
출력
The first and only line of output should contain integers (in any order)
representing events that have certainly occurred.
입출력 예
입력
3 2 1
1 2
2 3
2
출력
1 2 3
입력
3 2 1
1 3
2 3
3
출력
3
입력
4 4 1
1 2
1 3
2 4
3 4
4
출력
1 2 3 4
Explanation of the second sample case:
The knowledge base contains implications 1 -> 3 and 2 -> 3. Therefore,
Holmes knows that event 3 can be caused only by events 1 and 2, but
(without any extra information), he can't be certain which one of those
events actually caused 3. As a result, only event that must have occurred is
the one given in the input.
Explanation of the third sample case:
Holmes doesn't know which event from the set {2, 3} is directly responsible
for event 4. However, as both of those events are caused only by event 1,
Holmes can deduce that event 1 must have occurred. As a consequence,
events 2, 3 and 4 (given by the detectives) have also occurred.
출처:coci
[질/답]
[제출 현황]
[푼 후(0)]


