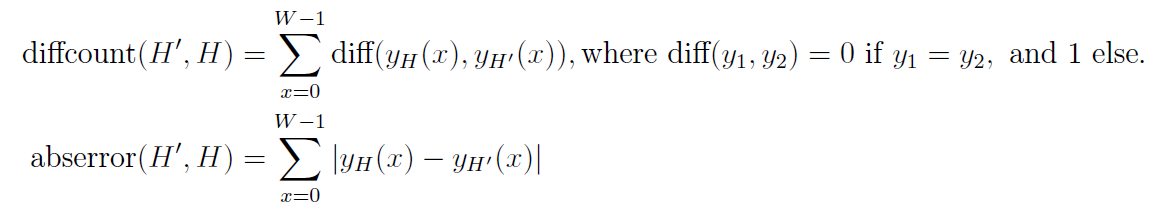프로그램 명: coci_histogrami(sepcial judge)
제한시간: 1 초

//sj 가 아직 되지 않았습니다.

히스토그램은 자료의 통계학적 특성을 시각적으로 표현한 그래프이다. 너비가 W인 히스토그램은 0~1, 1~2, …, W~W-1 범위의 자료의 수(도수)를 도표로 나타낸 것인데, 이를 점의 수가 N인 다각형으로 나타내면 아래와 같다. (단, N은 짝수)

(x0, y1), (x1, y1), (x2, y1), …, (xN/2-1, yN/2), (xN/2, yN/2)

또한, 다각형이 히스토그램이려면 다음 다섯 가지 조건을 더 만족해야 한다.

  1. x0 = 0 - 히스토그램은 직선 x=0에서 시작해야 한다.
  2. xN/2 = W - 히스토그램은 직선 x=W에서 끝나야 한다.
  3. xi < xi+1 - 히스토그램의 x좌표는 증가하는 순으로 이루어져 있다.
  4. yi > 0 - 히스토그램의 높이는 항상 0보다 커야 한다.
  5. yi ≠ yi+1 - 세로 선분의 길이는 항상 0보다 커야 한다.
당신은 주어진 히스토그램이 너무 복잡해서 유사 히스토그램을 만들려고 한다. 유사 히스토그램의 꼭짓점은 당신이 원하는 M개의 점들 중에서만 있어야 한다.

한편, 기존 히스토그램과 유사 히스토그램의 오차는 아래 두 가지 방법으로 계산한다.

  1. diffcount : W개의 구간 (0~1, …, W-1~W)들 중 도수가 다른 것들의 개수
  2. abserror : W개의 구간 (0~1, …, W-1~W)에 대해서 기존 히스토그램과 유사 히스토그램의 도수의 차이의 합
당신은 기존 히스토그램과의 오차가 가장 작은 히스토그램을 만들어야 한다. 예를 들어, 기존 히스토그램과 N개의 점들이 아래 그림과 같이 주어졌을 때, 두 번째 그림과 같이 히스토그램을 만들면 diffcount가 5로 최소가 되며, 세 번째 그림과 같이 히스토그램을 만들면 abserror가 14로 최소이다.

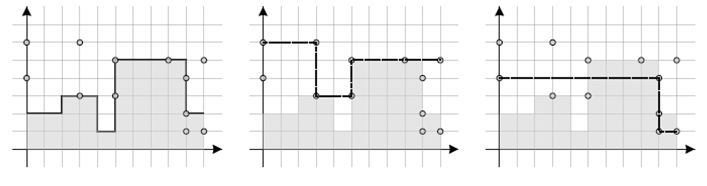
기존 히스토그램과 M개의 점들이 주어졌을 때, 기존 히스토그램과의 오차가 가장 작은 히스토그램을 구하는 프로그램을 작성하여라.

입력 형식

  1. 첫 번째 줄에는 기존 히스토그램의 꼭짓점의 수 N, 점들의 수 M, 오차 책정 방식 G가 주어진다. G=1이면 diffcount가 최소인 히스토그램을 구해야 하며, G=2이면 abserror가 최소인 히스토그램을 구해야 한다. (2 ≤ N ≤ 100,000, 2 ≤ M ≤ 100,000, G = 1 or 2, N은 짝수)
  2. 두 번째 줄부터 N개의 줄에는 기존 히스토그램의 꼭짓점의 좌표가 주어진다. 입력 데이터는 앞에서 언급했던 조건을 모두 만족해야 한다.
  3. N+2번째 줄부터 M개의 줄에는 M개의 점들의 좌표가 주어진다. 이 점들을 가지고 적어도 1개 이상의 히스토그램을 만들 수 있다. 모든 좌표는 0 이상 1,000,000 이하이다.
전체 데이터의 50%는 G=1이다. 그중 50%는 M ≤ 5,000이다.
전체 데이터의 50%는 G=2이다. 그중 50%는 M ≤ 5,000이다.

출력 형식

  1. 첫 번째 줄에는 오차의 최솟값을 출력한다.
  2. 두 번째 줄에는 유사 히스토그램의 점의 수를 출력한다. 이 값은 짝수여야 한다.
  3. 세 번째 줄부터는 유사 히스토그램의 꼭짓점의 좌표를 한 줄에 하나씩 출력한다. 출력 데이터 역시 앞에서 언급했던 조건을 모두 만족해야 한다.
답이 여러 개이면 그중 아무거나 출력한다. 
입력 예 1

10 12 1
0 2
2 2
2 3
4 3
4 1
5 1
5 5
9 5
9 2
10 2
0 4
0 6
3 3
3 6
9 4
9 1
5 3
5 5
10 5
9 2
10 1
8 5

출력 예 1

5
6
0 6
3 6
3 3
5 3
5 5
10 5
   
입력 예 2

10 12 2
0 2
2 2
2 3
4 3
4 1
5 1
5 5
9 5
9 2
10 2
0 4
0 6
3 3
3 6
9 4
9 1
5 3
5 5
10 5
9 2
10 1
8 5

출력 예 2

14
4
0 4
9 4
9 1
10 1
A histogram is a graphical representation of a statistical distribution of data. In other words, it is a function that assigns a positive integer value to each number in the interval 0; 1; 2; : : : ;W .. 1. For this task, we describe a histogram with a series of points in the standard coordinate system which, sequentially, determine the top edge of the area that the histogram encloses.

More specifically, we define a histogram of width W with an even number of points in the form:

(x0, y1), (x1, y1), (x1, y2), (x2, y2), (x2, y3).... (xN/2-1, yN/2), (xN/2, yN/2):
Therefore, starting from the first point, for every pair of adjacent points it must hold that their y coordinates are equal and that their x coordinates are equal. Thus, the histogram begins and ends with a horizontal segment and in between horizontal and vertical segments alternate. Additionally, the following holds for the shape of a histogram:
  1. x0 = 0 - the histogram begins on the line x = 0.
  2. xN/2 = W - the histogram ends on the line x = W.
  3. xi < xi+1, for each i = 1, 2...;N/2-1 - the histogram is defined from left to right and the length of each horizontal segment is at least one.
  4. yi > 0 - the height of the histogram is always greater than zero.
  5. yi != yi+1 - the length of each vertical segment is at least one.
For a histogram H, let yH(x) be the height of the histogram in the interval . For example, the surface area which the histogram encloses can be calculated by formula PW..1 x=0 yH(x). If two histograms, H and H0, are given, with equal width W (which can possibly be defined with a different number of points), then we can measure the difference between these two histograms in various ways. This measure of difference between two histograms is also called inaccuracy of histogram H’ with regard to histogram H. In this task, we examine two different ways of measuring differences between two histograms and we define them in the following way:

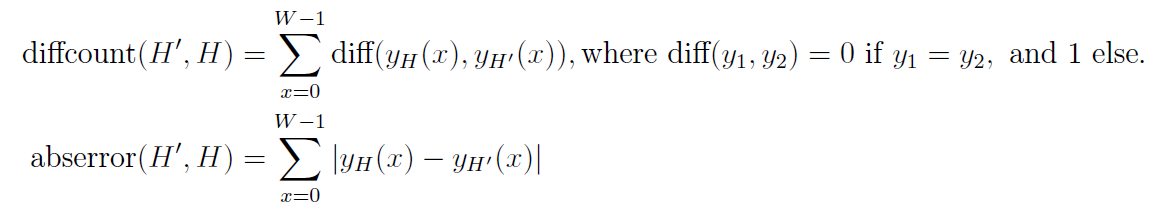
In other words, the first way measures the number of unit segments in which the two histograms differ, whereas the second way is the sum of absolute values of differences on those individual unit segments.

Write a program that will, for a given histogram H, set of points S and way of measuring inaccuracy, find and output histogram H0 which only uses points from the set S in its definition and has the least possible inaccuracy with regard to the given histogram

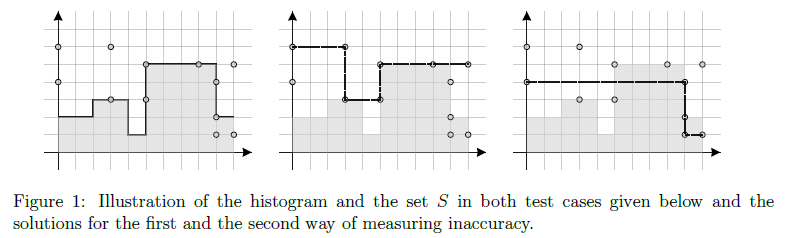
The definition of histogram H' must comply with all aforementioned conditions (for example, there shouldn’t be two continuous horizontal segments in the definition of histogram H0), and each point in the definition must be one of the points from the set S.

입력

출력

The first line of output must contain the least possible inaccuracy D. The second line of output must contain an even integer L - the total number of points in the definition of the required optimal histogram. In each of the following L lines, output two integers X and Y - coordinates of the point in the histogram’s definition.

The histogram’s definition must comply to all the conditions from the task. Please note: The solution may not be unique, but the input data will be such that there is always at least one solution.

SCORING

If the histogram’s definition is incorrect or wasn’t output, but the first line of output is correct (minimal inaccuracy), your solution will get 70% of total points for that test case.

In test cases worth 50 points, it will hold G = 1. In part of those test cases worth 25 points, it will additionally hold M <= 5 000.

In test cases worth 50 points, it will hold G = 2. In part of these test cases worth 25 points, it will additionally hold M <= 5 000.

입출력 예

input

10 12 1
0 2
2 2
2 3
4 3
4 1
5 1
5 5
9 5
9 2
10 2
0 4
0 6
3 3
3 6
9 4
9 1
5 3
5 5
10 5
9 2
10 1
8 5

output

5
6
0 6
3 6
3 3
5 3
5 5
10 5

input 

10 12 2
0 2
2 2
2 3
4 3
4 1
5 1
5 5
9 5
9 2
10 2
0 4
0 6
3 3
3 6
9 4
9 1
5 3
5 5
10 5
9 2
10 1
8 5

output

14
4
0 4
9 4
9 1
10 1

출처:coci/2013-2014/contest7
번역:functionx
[질/답] [제출 현황] [푼 후(0)]
[ 채 점 ] [홈으로]  [뒤 로]