N개의 노드와 M개의 간선이 있는 방향 그래프가 있다. 각 간선에는 자연수의 가중치가 매겨져 있다.

그런데, 어떤 간선의 가중치는 'X'라는 복면으로 가려져 있어서 가중치가 몇인지 알 수 없다. 그러나 복면으로 가려져 있는 간선은 모두 똑같은 자연수 가중치를 나타낸다.

시작점과 끝점이 주어질 때, 시작점에서 끝점으로 가는 최적의 경로(가중치의 합이 최소인 경로)의 가중치의 합으로 가능한 값의 개수와, 그 합을 구하는 프로그램을 작성하여라.

입력 형식

• 첫 번째 줄에 노드의 수 N과 간선의 수 M이 주어진다. (1 ≤ N ≤ 500, 0 ≤ M ≤ 10,000)
• 두 번째 줄부터 M개의 줄에는 각 간선의 시작점, 끝점, 가중치가 주어진다. 복면으로 가려진 간선의 가중치는 'X'로 주어지며, 안 가려진 간선의 가중치는 1,000,000 이하의 자연수이다.
• M+2번째 줄에는 테스트 케이스의 수 Q가 주어진다. (1 ≤ Q ≤ 10)
• 그 다음 줄부터 Q개의 줄에는 경로를 알아보려는 시작점의 번호 A와 끝점의 번호 B가 주어진다. (1 ≤ A, B ≤ N, A ≠ B)

출력 형식

입출력 예

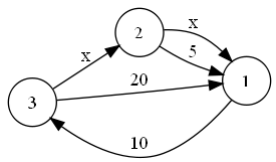
입력

4 4 
1 2 x 
2 3 x 
3 4 x 
1 4 8 
3 
2 1 
1 3 
1 4 

출력

0 0 
inf 
3 17 

입력

3 5 
3 2 x 
2 1 x 
2 1 5 
1 3 10 
3 1 20 
6 
1 2 
2 3 
3 1 
2 1 
3 2 
1 3 

출력

inf 
5 65 
15 185 
5 15 
inf 
1 10


1) 2번 노드에서 1번 노드로 가는 경로가 없으므로 0 0을 출력한다.
2) 모든 짝수가 1번 노드에서 3번 노드로 가는 최적의 경로의 가중치의 합으로 가능하므로 inf를 출력한다.
3) 1번 노드에서 4번 노드로 가는 최적의 경로의 가중치의 합으로 가능한 수는 3(x=1), 6(x=2), 8(x≥3)으로 3가지이며, 이들의 합은 17이다.

출처:CROATIAN olympiad 2013
번역:functionx